题目内容
14.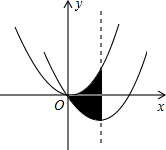 如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,求其对称轴与两段抛物线所围成的阴影部分的面积.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,求其对称轴与两段抛物线所围成的阴影部分的面积.
分析 确定出抛物线y=$\frac{1}{2}$x2-2x的顶点坐标,然后求出抛物线的对称轴与原抛物线的交点坐标,从而判断出阴影部分的面积等于三角形的面积,再根据三角形的面积公式列式计算即可得解.
解答 解:如图: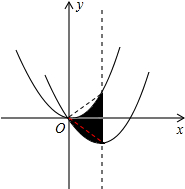 ,
,
∵y=$\frac{1}{2}$x2-2x=$\frac{1}{2}$(x-2)2-2,
∴平移后抛物线的顶点坐标为(2,-2),对称轴为直线x=2,
当x=2时,y=$\frac{1}{2}$×22=2,
∴平移后阴影部分的面积等于如图三角形的面积,
$\frac{1}{2}$×(2+2)×2=4,
答:其对称轴与两段抛物线所围成的阴影部分的面积4.
点评 本题考查了二次函数图象与几何变换,确定出与阴影部分面积相等的三角形是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
19.下列算式中正确的是( )
| A. | -x3-(-x)3=0 | B. | x+x2=x3 | C. | x6÷x3=x2 | D. | -x(x-1)=x2+1 |
 如图,B处在A处的南偏西40°方向,C处在A处的南偏东12°方向,C处在B处得北偏东80°方向,则∠ACB的度数为88度.
如图,B处在A处的南偏西40°方向,C处在A处的南偏东12°方向,C处在B处得北偏东80°方向,则∠ACB的度数为88度.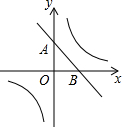 已知直线y=-x+b与双曲线y=$\frac{k}{x}$(k>0).
已知直线y=-x+b与双曲线y=$\frac{k}{x}$(k>0).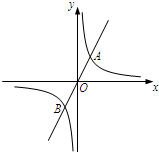 如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于点A、B,AB=2$\sqrt{5}$,
如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于点A、B,AB=2$\sqrt{5}$,