题目内容
19.已知四边形ABCD的四边分别是a,b,c,d,且a4+b4+c4+d4=4abcd,求证:四边形ABCD是菱形.分析 本题需先根据已知条件得出a4+b4+c4+d4-4abcd=0,然后再进行整理,得出(a2-b2)2+(c2-d2)2+2(ab-cd)2=0,再根据a,b,c,d都是正数这个条件,得出a=b,c=d,a=c,最后得出该四边形的四条边相等,则四边形ABCD是菱形.
解答 证明:由已知可得:a4+b4+c4+d4-4abcd=0,
(a2-b2)2+(c2-d2)2+2a2b2+2c2d2-4abcd=0,
∴(a2-b2)2+(c2-d2)2+2(ab-cd)2=0.
∴(a2-b2)2≥0,(c2-d2)2≥0,(ab-cd)2≥0,
∴a2-b2=c2-d2=ab-cd=0,
∴(a+b)(a-b)=(c+d)(c-d)=0.
又∵a,b,c,d都为正数,
∴a+b≠0,c+d≠0,
∴a=b,c=d.
∴ab-cd=a2-c2=(a+c)(a-c)=0,
∴a=c,
∴a=b=c=d,即四边形ABCD是菱形.
点评 本题主要考查了菱形的判定,利用了“四条边相等的四边形为菱形”的判定定理证得结论,在解题时要注意采用综合法去证明这是解题的关键.

练习册系列答案
相关题目
9.下列说法中,正确的有( )
①角的大小随边的长度变化而变化
②若AD是∠BAC的平分线,则∠BAD=∠DAC
③一个有理数不是整数就是分数
④若一个角既有余角又有补角,则它的补角一定比它的余角大.
①角的大小随边的长度变化而变化
②若AD是∠BAC的平分线,则∠BAD=∠DAC
③一个有理数不是整数就是分数
④若一个角既有余角又有补角,则它的补角一定比它的余角大.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.下列计算正确的是( )
| A. | (a-$\frac{1}{2}$b)2=a2-$\frac{1}{2}$ab+$\frac{1}{4}$b2 | B. | -2a2($\frac{1}{2}$ab+b2)=-a3b+b2a2 | ||
| C. | -$\frac{1}{2}$a2bn•(3anbn+1)=-$\frac{3}{2}$a2nb${\;}^{{n}^{2}+n}$ | D. | (a-b)(-a-2b)=-a2-ab+2b2 |
11.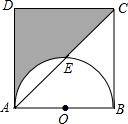 如图所示,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为( )
如图所示,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为( )
 如图所示,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为( )
如图所示,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为( )| A. | 10-π | B. | 8-π | C. | 12-π | D. | 6-π |
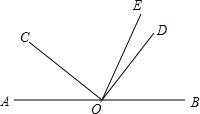 已知:O是直线AB上一点,∠COD是直角,OE平分∠BOC
已知:O是直线AB上一点,∠COD是直角,OE平分∠BOC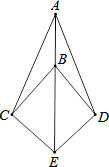 如图,点B在线段AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:EC=ED.
如图,点B在线段AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:EC=ED.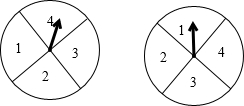 让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和概率最大的和等于( )
让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和概率最大的和等于( )