题目内容
8.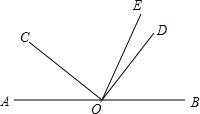 已知:O是直线AB上一点,∠COD是直角,OE平分∠BOC
已知:O是直线AB上一点,∠COD是直角,OE平分∠BOC(1)若∠AOC=30°,求∠DOE的度数;
(2)若∠AOC=α,请直接写出∠DOE的度数(用含α的代数式表示);
(3)若OD将∠BOE分为1:2的两个角,求∠AOC.
分析 (1)求出∠BOD,求出∠BOC,根据角平分线求出∠BOE,代入∠DOE=∠BOE-∠BOD求出即可.
(2)求出∠BOD,求出∠BOC,根据角平分线求出∠BOE,代入∠DOE=∠BOE-∠BOD求出即可.
(3)把∠DOE当作已知数求出∠DOB,根据角平分线求出∠BOC,代入∠COD=∠COE+∠DOE=90°求出即可.
解答 解:(1)∵∠COD是直角,∠AOC=30°,
∴∠BOD=180°-90°-30°=60°,
∴∠COB=90°+60°=150°,
∵OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠BOC=75°,
∴∠DOE=∠BOE-∠BOD=75°-60°=15°.
(2)∵∠COD是直角,∠AOC=α,
∴∠BOD=180°-90°-α=90°-α,
∴∠COB=90°+90°-α=180°-α,
∵OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠BOC=90°-$\frac{1}{2}$α,
∴∠DOE=∠BOE-∠BOD=90°-$\frac{1}{2}$α-(90°-α)=$\frac{1}{2}$α.
(3)当∠DOE:∠BOD=1:2时,设∠AOC=α,
∴∠BOD=180°-90°-α=90°-α,
∴∠COB=90°+90°-α=180°-α,
∵OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠BOC=90°-$\frac{1}{2}$α,
∴∠DOE=∠BOE-∠BOD=90°-$\frac{1}{2}$α-(90°-α)=$\frac{1}{2}$α
则$\frac{1}{2}$α×2=90°-α,解得α=45°
当∠DOE:∠BOD=2:1时,设∠AOC=α,
∴∠BOD=180°-90°-α=90°-α,
∴∠COB=90°+90°-α=180°-α,
∵OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠BOC=90°-$\frac{1}{2}$α,
∴∠DOE=∠BOE-∠BOD=90°-$\frac{1}{2}$α-(90°-α)=$\frac{1}{2}$α
则有$\frac{1}{2}$α=2(90°-α),解得α=72°.
点评 本题考查了角的有关计算和角平分线定义的应用,应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
 如图,△ABC中,DE是边AB的垂直平分线,AD=9,BC=11,AB=14,则BD的长是( )
如图,△ABC中,DE是边AB的垂直平分线,AD=9,BC=11,AB=14,则BD的长是( )| A. | 9 | B. | 11 | C. | 14 | D. | 无法确定 |
 如图,在平行四边形ABCD中,AC、BD交于点O,已知∠ODA=90°,OB=2,OA=4,求平行四边形ABCD的周长和面积.
如图,在平行四边形ABCD中,AC、BD交于点O,已知∠ODA=90°,OB=2,OA=4,求平行四边形ABCD的周长和面积.