题目内容
一只不透明的袋子中,装有2个白球和1个红球,这些球除颜色外其他都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球是等可能的.你同意他的说法吗?为什么?
(2)搅匀后从中摸出一个球,请求出不是白球的概率;
(3)搅匀后从中任意摸出一个球,要使摸出红球的概率为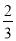 ,应添加几个红球?
,应添加几个红球?
 (1)不同意,理由见解析;(2);(3)3.
【解析】试题分析:(1)求出分别摸到白球与摸到红球的概率,比较这两个概率,即可知道谁的可能性大,概率大则可能性就大;
(2)由(1)即可得出结论;
(3)此题考查了借助方程思想求概率的问题,解题的关键是找到等量关系.
试题解析:【解析】
(1)不同意,因为两种球数量不同,装有2个白球和1个红球,摸出白球的概率为,摸出红球的概率...
(1)不同意,理由见解析;(2);(3)3.
【解析】试题分析:(1)求出分别摸到白球与摸到红球的概率,比较这两个概率,即可知道谁的可能性大,概率大则可能性就大;
(2)由(1)即可得出结论;
(3)此题考查了借助方程思想求概率的问题,解题的关键是找到等量关系.
试题解析:【解析】
(1)不同意,因为两种球数量不同,装有2个白球和1个红球,摸出白球的概率为,摸出红球的概率...
练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
如图,已知线段a,c,∠α.
求作△ABC,使BC=a,AB=c,∠ABC=∠α.
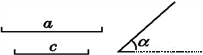
 见解析
【解析】【试题分析】利用“SAS”原理作图.
【试题解析】
(1)作∠MBN=∠α.
(2)在射线BM上截取BA=c,在射线BN上截取BC=a.
(3)连接AC,则△ABC即为所求作的三角形(如图).
见解析
【解析】【试题分析】利用“SAS”原理作图.
【试题解析】
(1)作∠MBN=∠α.
(2)在射线BM上截取BA=c,在射线BN上截取BC=a.
(3)连接AC,则△ABC即为所求作的三角形(如图). 下列平移作图错误的是( ).
A. 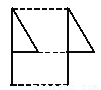 B.
B. 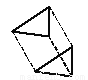 C.
C.  D.
D. 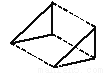
 C
【解析】试题分析:A、B、D符合平移变换,C是轴对称变换.
故选C.
C
【解析】试题分析:A、B、D符合平移变换,C是轴对称变换.
故选C. 计算cos80°﹣sin80°的值大约为( )
A. 0.8111 B. ﹣0.8111 C. 0.8112
 B
【解析】根据一个角的余弦等于它余角的正弦,可转化成正弦函数,根据锐角的正弦随角的度数的增大而增大,可得答案,
cos80°﹣sin80°=sin10°-sin80°<0,
观察可知只有B选项符合,
故选B.
B
【解析】根据一个角的余弦等于它余角的正弦,可转化成正弦函数,根据锐角的正弦随角的度数的增大而增大,可得答案,
cos80°﹣sin80°=sin10°-sin80°<0,
观察可知只有B选项符合,
故选B. 利用计算器求tan45°时,依次按键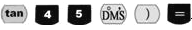 则计算器上显示的结果是( )
则计算器上显示的结果是( )
A. 0.5 B. 0.707 C. 0.866 D. 1
 D
【解析】试题分析:依次按键则计算器上显示的是tan45°的值,即1.
故选D.
D
【解析】试题分析:依次按键则计算器上显示的是tan45°的值,即1.
故选D. 已知a+b=-5,ab=7,求a2+b2的值.
 11
【解析】试题分析:根据完全平方公式的变形进行计算即可.
试题解析:【解析】
因为a+b=-5,ab=7,
所以a2+b2=(a+b)2-2ab=(-5)2-2×7=11.
11
【解析】试题分析:根据完全平方公式的变形进行计算即可.
试题解析:【解析】
因为a+b=-5,ab=7,
所以a2+b2=(a+b)2-2ab=(-5)2-2×7=11. 如图,点D,E是正三角形ABC的边BC,AC上的点,且CD=AE,AD,BE相交于点P,BQ⊥AD于点Q,已知BE=7,则AD等于( )
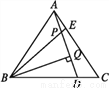
A. 5 B. 6 C. 7 D. 8
 C
【解析】【解析】
∵△ABC是等边三角形,∴AB=AC,∠BAC=∠C=60°.
又∵AE=CD,∴△ABE≌△CAD(SAS),∴AD=BE=7.
故选C.
C
【解析】【解析】
∵△ABC是等边三角形,∴AB=AC,∠BAC=∠C=60°.
又∵AE=CD,∴△ABE≌△CAD(SAS),∴AD=BE=7.
故选C. 对于解不等式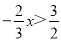 ,正确的结果是( )
,正确的结果是( )
A.x<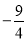 B.x>
B.x>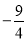 C.x>-1 D.x<-1
C.x>-1 D.x<-1
 A.
【解析】
试题分析:先去分母得,-4x>9,再把x的系数化为1得,x<.
故选A.
A.
【解析】
试题分析:先去分母得,-4x>9,再把x的系数化为1得,x<.
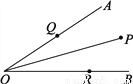
故选A. 如图,∠AOB=30°,角内有一点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长的最小值是多少?
 10cm
【解析】试题分析:设点P关于OA的对称点是E,关于OB的对称点是F,当点R、Q在EF上时,△PQR的周长=PQ+QR+PR=EF,此时周长最小.
试题解析:作出点P关于OA的对称点E,作出点P关于OB的对称点F,连接EF,交OA于Q,交OB于R.连接PQ,PR,PE,PF,OE,OF,
则PQ=EQ,PR=RF,
则△PQR的周长=PQ+QR+PR=EQ+QR+R...
10cm
【解析】试题分析:设点P关于OA的对称点是E,关于OB的对称点是F,当点R、Q在EF上时,△PQR的周长=PQ+QR+PR=EF,此时周长最小.
试题解析:作出点P关于OA的对称点E,作出点P关于OB的对称点F,连接EF,交OA于Q,交OB于R.连接PQ,PR,PE,PF,OE,OF,
则PQ=EQ,PR=RF,
则△PQR的周长=PQ+QR+PR=EQ+QR+R... 
