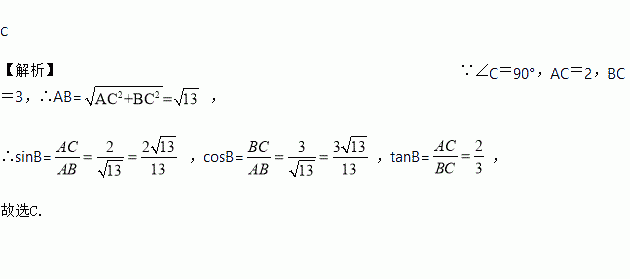题目内容
在Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中,正确的是( )
A. sin B=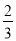 B. cos B=
B. cos B=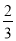 C. tan B=
C. tan B=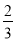 D. tan B=
D. tan B=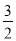
 C
【解析】∵∠C=90°,AC=2,BC=3,∴AB= ,
∴sinB= ,cosB=,tanB=,
故选C.
C
【解析】∵∠C=90°,AC=2,BC=3,∴AB= ,
∴sinB= ,cosB=,tanB=,
故选C.
练习册系列答案
相关题目
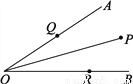
如图,∠AOB=30°,角内有一点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长的最小值是多少?
 10cm
【解析】试题分析:设点P关于OA的对称点是E,关于OB的对称点是F,当点R、Q在EF上时,△PQR的周长=PQ+QR+PR=EF,此时周长最小.
试题解析:作出点P关于OA的对称点E,作出点P关于OB的对称点F,连接EF,交OA于Q,交OB于R.连接PQ,PR,PE,PF,OE,OF,
则PQ=EQ,PR=RF,
则△PQR的周长=PQ+QR+PR=EQ+QR+R...
10cm
【解析】试题分析:设点P关于OA的对称点是E,关于OB的对称点是F,当点R、Q在EF上时,△PQR的周长=PQ+QR+PR=EF,此时周长最小.
试题解析:作出点P关于OA的对称点E,作出点P关于OB的对称点F,连接EF,交OA于Q,交OB于R.连接PQ,PR,PE,PF,OE,OF,
则PQ=EQ,PR=RF,
则△PQR的周长=PQ+QR+PR=EQ+QR+R... 分式方程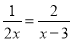 的解是_____.
的解是_____.
 x=﹣1
【解析】试题分析:根据解分式方程的方法可以求得分式方程的解,记住最后要进行检验,本题得以解决.
【解析】
方程两边同乘以2x(x﹣3),得
x﹣3=4x
解得,x=﹣1,
检验:当x=﹣1时,2x(x﹣3)≠0,
故原分式方程的解是x=﹣1,
故答案为:x=﹣1.
x=﹣1
【解析】试题分析:根据解分式方程的方法可以求得分式方程的解,记住最后要进行检验,本题得以解决.
【解析】
方程两边同乘以2x(x﹣3),得
x﹣3=4x
解得,x=﹣1,
检验:当x=﹣1时,2x(x﹣3)≠0,
故原分式方程的解是x=﹣1,
故答案为:x=﹣1. 如图,正方形ABCD的边长为4,点M在边DC上,M,N两点关于对角线AC对称,若DM=1,则tan∠ADN=________.
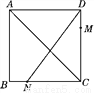
 【解析】试题分析:在正方形ABCD中,AB=CD.由M、N两点关于对角线AC对称,所以DM=BN=1, 再由题意可知tan∠AND===tan(90°-∠CDN),进而求出CN=BC-BN=4-1=3.再由题意可知tan∠AND=tan(90°-∠CDN)===.
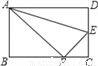
【解析】试题分析:在正方形ABCD中,AB=CD.由M、N两点关于对角线AC对称,所以DM=BN=1, 再由题意可知tan∠AND===tan(90°-∠CDN),进而求出CN=BC-BN=4-1=3.再由题意可知tan∠AND=tan(90°-∠CDN)===. 如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处已知AB=8,BC=10,则tan∠EFC的值为( )
A. 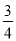 B.
B. 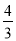 C.
C. 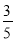 D.
D. 
 A
【解析】试题解析:根据题意可得:在Rt△ABF中,有AB=8,AF=AD=10,BF=6,
而Rt△ABF∽Rt△EFC,故有∠EFC=∠BAF,故tan∠EFC=tan∠BAF=.
故选A.
A
【解析】试题解析:根据题意可得:在Rt△ABF中,有AB=8,AF=AD=10,BF=6,
而Rt△ABF∽Rt△EFC,故有∠EFC=∠BAF,故tan∠EFC=tan∠BAF=.
故选A. 分解因式:6x-4xy
 2x(3-2y)
【解析】试题分析:根据提公因式法分解因式,先确定公因式2x,再提取公因式即可.
试题解析:6x-4xy=2x(3-2y).
2x(3-2y)
【解析】试题分析:根据提公因式法分解因式,先确定公因式2x,再提取公因式即可.
试题解析:6x-4xy=2x(3-2y). 把多项式-x2+x提取公因式-x后,余下的部分是( )
A. x B. x-1 C. x+1 D. x2
 B
【解析】根据因式分解的提公因式,提取公因式-x,可得-x2+x=-x(x-1),所以剩余部分为x-1.
故选:B.
B
【解析】根据因式分解的提公因式,提取公因式-x,可得-x2+x=-x(x-1),所以剩余部分为x-1.
故选:B. 下列说法正确的是 ( )
A. 两个全等的图形可看做其中一个是由另一个平移得到的
B. 由平移得到的两个图形对应点连线互相平行(或共线)
C. 由平移得到的两个等腰三角形周长一定相等,但面积未必相等
D. 边长相等的两个正方形一定可以通过平移得到
 B
【解析】试题分析:A、全等三角形仅仅是反映了两个三角形的形状和大小关系,而平移既需要两个三角形全等,还需要两个三角形有一种特殊的位置关系,故错误;
B、符合平移的性质,故正确;
C、由平移得到的两个等腰三角形全等,面积必相等,故错误;
D、平移还需要具备一种特殊的位置关系,故错误.
故选B.
B
【解析】试题分析:A、全等三角形仅仅是反映了两个三角形的形状和大小关系,而平移既需要两个三角形全等,还需要两个三角形有一种特殊的位置关系,故错误;
B、符合平移的性质,故正确;
C、由平移得到的两个等腰三角形全等,面积必相等,故错误;
D、平移还需要具备一种特殊的位置关系,故错误.
故选B. 如图,△ABC沿MN方向平移3cm后,成为△DEF那么点A的对应点是哪个点?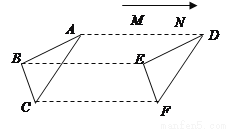
 D点.
【解析】试题分析:△ABC沿MN方向平移3cm后,成为△DEF,即可得到对应点的关系.试题解析:A点沿MN的方向平移3cm后对应点是D点.
D点.
【解析】试题分析:△ABC沿MN方向平移3cm后,成为△DEF,即可得到对应点的关系.试题解析:A点沿MN的方向平移3cm后对应点是D点.