Question

18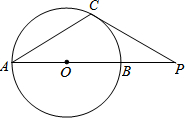．如图，AB是⊙O的直径，点P在AB的延长线上，PC切⊙O于点C，若AB=8，∠CPA=30°，则PC的长等于4$\sqrt{3}$．

Answer 1

分析 连接OC，由切线的性质可知△OCP是直角三角形，又因为OC的长可求出，∠CPA=30°，所以PC的长即可求出．

解答 解：连接OC，
∵PC切⊙O于点C，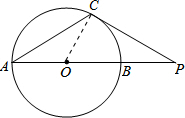
∴OC⊥CP，
∴△OCP是直角三角形，
∵AB=8，
∴OC=4，
∵∠CPA=30°，
∴PC=4$\sqrt{3}$，
故答案为：4$\sqrt{3}$．

点评 本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．