题目内容
11.m是$\sqrt{13}$的整数部分,n是$\sqrt{13}$的小数部分,求(m-n)2的值.分析 因为3<$\sqrt{13}$<4,所以$\sqrt{13}$的整数部分m=3,则小数部分n=$\sqrt{13}$-3,进一步把代数式化简,代入求值即可.
解答 解:∵3<$\sqrt{13}$<4,
∴$\sqrt{13}$的整数部分m=3,则小数部分n=$\sqrt{13}$-3,
∴(m-n)2=${(3-\sqrt{13}+3)}^{2}$=49$+12\sqrt{13}$.
点评 此题考查无理数的估算方法,代数式求值等知识点,注意利用夹逼法得出m,n的值是解答此题的关键.

练习册系列答案
相关题目
18.如果一个实数的算术平方根等于它的立方根,那么满足条件的实数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
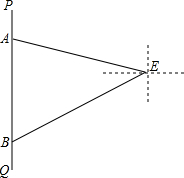 如图,灯塔E到一段南北向航线PQ的距离为10海里,一艘船沿此航线由北向南航行,在点A在灯塔E的北偏西68°方向,点B处在灯塔E西南方向,求轮AB的距离(精确到0.1海里/时).
如图,灯塔E到一段南北向航线PQ的距离为10海里,一艘船沿此航线由北向南航行,在点A在灯塔E的北偏西68°方向,点B处在灯塔E西南方向,求轮AB的距离(精确到0.1海里/时).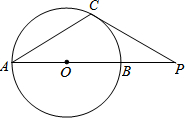 如图,AB是⊙O的直径,点P在AB的延长线上,PC切⊙O于点C,若AB=8,∠CPA=30°,则PC的长等于4$\sqrt{3}$.
如图,AB是⊙O的直径,点P在AB的延长线上,PC切⊙O于点C,若AB=8,∠CPA=30°,则PC的长等于4$\sqrt{3}$.