题目内容
10.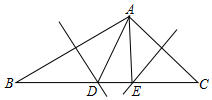 如图,在△ABC中,线段AB、AC的垂直平分线与BC的交点分别为D、E.
如图,在△ABC中,线段AB、AC的垂直平分线与BC的交点分别为D、E.(1)若△ADE的周长是15,求BC的长;
(2)若∠BAC=100°,求∠DAE的度数.
分析 (1)根据线段的垂直平分线的性质,即可得到AD=BD,AE=CE,再根据AD+DE+AE=15,即可得到BD+DE+CE=15;
(2)根据三角形内角和定理,即可得到∠B+∠C=80°,再根据∠B+∠BAD,∠C=∠CAE,即可得出∠BAD+∠CAE=80°,进而得到∠DAE=100°-80°=20°.
解答 解:(1)∵线段AB、AC的垂直平分线与BC的交点分别为D、E,
∴AD=BD,AE=CE,
∵△ADE的周长是15,
∴AD+DE+AE=15,
∴BD+DE+CE=15,即BC=15;
(2)∵∠BAC=100°,
∴△ABC中,∠B+∠C=80°,
又∵AD=BD,AE=CE,
∴∠B+∠BAD,∠C=∠CAE,
∴∠BAD+∠CAE=80°,
∴∠DAE=100°-80°=20°.
点评 本题主要考查了线段垂直平分线的性质的运用,解题时注意:线段垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
相关题目
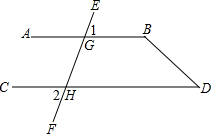 如图已知∠1=∠2,∠D=50°,
如图已知∠1=∠2,∠D=50°,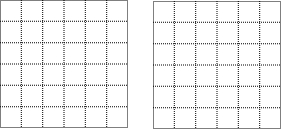 如图,正方形网络中的每个小正方形边长都为1,每个小正方形的顶点叫格点,分别按下列要求画以格点为顶点三角形和平行四边形.(无需写画法)
如图,正方形网络中的每个小正方形边长都为1,每个小正方形的顶点叫格点,分别按下列要求画以格点为顶点三角形和平行四边形.(无需写画法)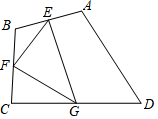 如图,四边形ABCD中,点E、F、G分别为边AB、BC、CD的中点,若△EFG的面积为4,则四边形ABCD的面积为( )
如图,四边形ABCD中,点E、F、G分别为边AB、BC、CD的中点,若△EFG的面积为4,则四边形ABCD的面积为( )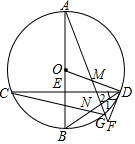 如图,在⊙O中,直径AB经过弦CD的中点E,点M在OD上,AM的延长线交⊙O于点G,交过D的直线于F,∠1=∠2,连结BD与CG交于点N.
如图,在⊙O中,直径AB经过弦CD的中点E,点M在OD上,AM的延长线交⊙O于点G,交过D的直线于F,∠1=∠2,连结BD与CG交于点N.