题目内容
3.已知二次函数y=mx2-(m+2)x+2的图象与x轴有两个不同的交点(x1,0)、(x2,0)(1)求m的取值范围;
(2)若x2<0,且$\frac{{x}_{1}}{{x}_{2}}$>-1,求整数m的值.
分析 (1)由二次项系数不为0,且根的判别式大于0,求出m的范围即可;
(2)利用求根公式表示出方程的解,根据题意确定出m的范围,找出整数m的值即可.
解答 解:(1)由已知得:m≠0且△=(m+2)2-8m=(m-2)2>0,
则m的范围为m≠0且m≠2;
(2)方程解得:x=$\frac{(m+2)±(m-2)}{2m}$,即x=1或x=$\frac{2}{m}$,
∵x2<0,∴x2=$\frac{2}{m}$<0,即m<0,
∵$\frac{{x}_{1}}{{x}_{2}}$>-1,
∴$\frac{m}{2}$>-1,即m>-2,
∵m≠0且m≠2,
∴-2<m<0,
∵m为整数,
∴m=-1.
点评 此题考查了根的判别式,一元二次方程有两个不相等的实数根即为根的判别式大于0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知反比例函数y=$\frac{m-3}{x}$的图象经过第一、三象限,则符合条件的m是( )
| A. | m=-1 | B. | m=0 | C. | m=3 | D. | m=5 |
15.下列函数中,经过一、二、四象限的函数是( )
| A. | y=7 | B. | y=-2x | C. | y=-2x-7 | D. | y=-2x+7 |
12.某教育主管部门深入边远山区,随机走访农户,调查农村儿童生活教育现状,根据收集的数据编制了不完整的统计图表如下:
山区儿童生活教育现状
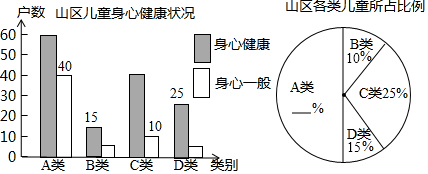
请你用学过的统计知识,解决问题:
(1)教育主管部门走访了边远山区多少家农户?
(2)将统计图表中的空缺数据填写完整;
(3)分析数据后,请你提一条合理建议.
山区儿童生活教育现状
| 类别 | 现状 | 户数 | 比例 |
| A类 | 父母长年在外打工,孩子留在老家由老人照顾 | 100 | |
| B类 | 父母长年在外打工,孩子带在身边 | 10% | |
| C类 | 父母就近在城镇打工,晚上回家照顾孩子 | 50 | |
| D类 | 父母在家务农,并照顾孩子 | 15% |

请你用学过的统计知识,解决问题:
(1)教育主管部门走访了边远山区多少家农户?
(2)将统计图表中的空缺数据填写完整;
(3)分析数据后,请你提一条合理建议.
18. 如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )
如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )
 如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )
如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )| A. | 50° | B. | 65° | C. | 75° | D. | 85° |
 小明在做课本“目标与评定”中的一道题:如图(1),直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图(1),画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.
小明在做课本“目标与评定”中的一道题:如图(1),直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图(1),画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.