题目内容
3.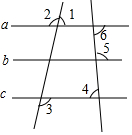 如图,下列命题是假命题的是( )
如图,下列命题是假命题的是( )| A. | 如果∠2=∠3,那么a∥c | B. | 如果a∥b,a∥c,那么b∥c | ||
| C. | 如果∠4+∠5=180°,那么∠2=∠3 | D. | 如果∠4=∠6,那么∠1+∠3=180° |
分析 根据平行线的性质,平行公理对各选项分析判断即可得解.
解答 解:A、∵∠2=∠3,
∴∠2的对顶角与∠3相等,
∴a∥c,是真命题,故本选项不符合题意;
B、∵a∥b,a∥c,
∴b∥c(平行公理),是真命题,故本选项不符合题意;
C、∵∠4+∠5=180°,
∴∠4与∠5的对顶角的和等于180°,
∴b∥c,
无法推出∠2=∠3,是假命题,故本选项符合题意;
D、∵∠4=∠6,
∴a∥c,
∴∠1的对顶角与∠3的对顶角的和等于180°,
∴∠1+∠3=180°,是真命题,故本选项不符合题意.
故选C.
点评 本题主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
相关题目
18. 如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )
如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )
 如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )
如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )| A. | 50° | B. | 65° | C. | 75° | D. | 85° |