题目内容
16.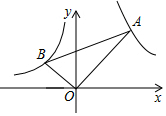 如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{2}{x}$,y=$\frac{8}{x}$的图象交于B、A两点,则tan∠OAB的值的变化趋势为:( )
如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{2}{x}$,y=$\frac{8}{x}$的图象交于B、A两点,则tan∠OAB的值的变化趋势为:( )| A. | 逐渐变小 | B. | 逐渐变大 | C. | 时大时小 | D. | 保持不变 |
分析 作辅助线;首先证明△BOM∽△OAN,得到$\frac{BM}{ON}$=$\frac{OM}{AN}$;设B(-m,$\frac{2}{m}$),A(n,$\frac{8}{n}$),得到BM=$\frac{2}{m}$,AN=$\frac{8}{n}$,OM=m,ON=n,进而得到mn=$\frac{16}{mn}$,mn=4,此为解决问题的关键性结论;运用三角函数的定义证明知tan∠OAB=$\frac{1}{2}$为定值,即可解决问题.
解答 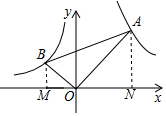 解:如图,分别过点A、B作AN⊥x轴、BM⊥x轴;
解:如图,分别过点A、B作AN⊥x轴、BM⊥x轴;
∵∠AOB=90°,
∴∠BOM+∠AON=∠AON+∠OAN=90°,
∴∠BOM=∠OAN,
∵∠BMO=∠ANO=90°,
∴△BOM∽△OAN,
∴$\frac{BM}{ON}$=$\frac{OM}{AN}$;
设B(-m,$\frac{2}{m}$),A(n,$\frac{8}{n}$),
则BM=$\frac{2}{m}$,AN=$\frac{8}{n}$,OM=m,ON=n,
∴mn=$\frac{16}{mn}$,mn=$\sqrt{16}$=4;
∵∠AOB=90°,
∴tan∠OAB=$\frac{OB}{OA}$①;
∵△BOM∽△OAN,
∴$\frac{OB}{OA}$=$\frac{BM}{ON}$=$\frac{\frac{2}{m}}{n}$=$\frac{2}{mn}$=$\frac{1}{2}$②,
由①②知tan∠OAB=$\frac{1}{2}$为定值,
∴∠OAB的大小不变,
故选:D.
点评 该题主要考查了反比例函数图象上点的坐标特征、相似三角形的判定等知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用相似三角形的判定等知识点来分析、判断、推理或解答.

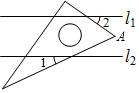 已知,直线l1∥l2,一块含30°角的直角三角尺如图放置,∠1=25°,则∠2等于( )
已知,直线l1∥l2,一块含30°角的直角三角尺如图放置,∠1=25°,则∠2等于( )| A. | 45° | B. | 40° | C. | 35° | D. | 30° |
| A. | 9m2-4n2=(9m+4n)(9m-4n) | B. | a2-4=(a-2)2 | ||
| C. | 9-6a+a2=(a-3)2 | D. | x2-3x+1=x(x-3)+1 |
| A. | $\sqrt{{a}^{2}+{b}^{2}}$ | B. | $\sqrt{\frac{a}{b}}$ | C. | $\sqrt{25a}$ | D. | $\sqrt{4a+4}$ |
 如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短,理由是( )
如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短,理由是( )| A. | 垂线段最短 | B. | 两点确定一条直线 | ||
| C. | 点到直线的距离 | D. | 两点之间线段最短 |

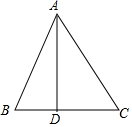 如图,在△ABC中,AB=26,BC=28,AC=30,求BC边上的高AD.
如图,在△ABC中,AB=26,BC=28,AC=30,求BC边上的高AD.