题目内容

4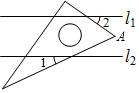．已知，直线l1∥l2，一块含30°角的直角三角尺如图放置，∠1=25°，则∠2等于（　　）
A．45°B．40°C．35°D．30°

分析 先根据三角形外角的性质求出∠3的度数，再由平行线的性质得出∠4的度数，由直角三角形的性质即可得出结论．

解答 解：∵∠3是△BDG的外角，
∴∠3=∠B+∠1=30°+25°=55°，
∵l1∥l2，
∴∠3=∠4=55°，
∵∠4+∠EFC=90°，
∴∠EFC=90°-55°=35°，
∴∠2=35°．
故选：C．

点评 本题考查的是平行线的性质及三角形外角的性质，用到的知识点为：两直线平行，同位角相等．

练习册系列答案
相关题目
18．计算：
（1）$\sqrt{8}$+2$\sqrt{3}$-（$\sqrt{27}$-$\sqrt{2}$）；
（2）（10$\sqrt{48}$-6$\sqrt{27}$+4$\sqrt{12}$）$÷\sqrt{12}$．
15．已知$\left\{\begin{array}{l}x=2\\ y=-3\end{array}$是关于x，y的二元一次方程3x=y+a的解，求a（a-1）的值．
12．把一张对边互相平行的纸条，折成如图所示，EF是折痕．若∠EFB=35°，则下面五个结论：①∠CEF=35°；②∠AEC=145°；③∠BGE=70°；④∠EFD′=110°；⑤∠D′FD=70°．其中正确的是①③⑤．（只填序号）
19．如图，直线AC∥BD，P在直线AB上（不与点A，B重合）．
（1）当点P在如图所示的位置时，∠PCA=30°，∠PDB=25°，则∠CPD=55°．
（2）猜想，当点P在A，B两点之间运动时，∠PCA，∠PDB，∠CPD之间的数量关系∠CPD=∠PCA+∠PDB．
（3）说明（2）中的猜想成立的理由．
（4）当点P在直线AB上（不在线段AB上）运动时，试探究∠PCA，∠PDB，∠CPD之间的数量关系（画图并直接写出结论即可）
9．在如图所示的正方形网格中，每个小正方形的边长均为1，格点三角形（顶点在网格线的交点处的三角形）ABC的顶点A、C的坐标系分别为A（-4，5）、C（-1，3）．
（1）请在所给的网格图内画出平面直角坐标系xOy；
（2）将△ABC向右平移4个单位，再向下平移2个单位，得到△A1B1C1，请你画出△A1B1C1，并分别写出A1，B1，C1的坐标；
（3）若P（a，b）是△ABC内的一点，P1是△A1B1C1中与P对应的点，则P1的坐标是（a+4，b-2）；
（4）△ABC的面积是4．
16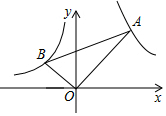．如图，在x轴的上方，直角∠BOA绕原点O按顺时针方向旋转，若∠BOA的两边分别与函数y=-$\frac{2}{x}$，y=$\frac{8}{x}$的图象交于B、A两点，则tan∠OAB的值的变化趋势为：（　　）
A．逐渐变小B．逐渐变大C．时大时小D．保持不变
13．如图（1），直线l⊥x轴于点P，Rt△ABC中，斜边AB=5，直角边AC=3，点A（0，t）在y轴上运动，直角边BC在直线l上，将△ABC绕点P顺时针旋转90°，得到△DEF．以直线l为对称轴的抛物线经过点F．
（1）求点F的坐标（用含t的式子表示）
（2）①如图（2）当抛物线的顶点为点C时，抛物线恰好过坐标原点．求此时抛物线的解析式；
②如图（3）不改变①中抛物线的开口方向和形状，让点A的位置发生变化，使抛物线与线段AB始终有交点M（x0，y0）．
（ⅰ）求t的取值范围；
（ⅱ）变化过程中，当x0变成某一个值时，点A的位置唯一确定，求此时点M的坐标．
14．若关于x的不等式（a-5）x＞2a-10的解集是x＜2，则a的取值范围是（　　）
A．a＜5B．a＞5C．a＜0D．a＞0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网