题目内容
8.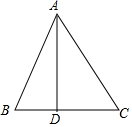 如图,在△ABC中,AB=26,BC=28,AC=30,求BC边上的高AD.
如图,在△ABC中,AB=26,BC=28,AC=30,求BC边上的高AD.
分析 设DC=x,则有BD=28-x,在直角三角形ABD与直角三角形ACD中,利用勾股定理列出方程,求出方程的解得到x的值,即可确定出AD的长.
解答 解:设DC=x,则BD=28-x,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:AB2-BD2=AD2=AC2-CD2,
即262-(28-x)2=302-x2,
解得:x=18,
则AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{3{0}^{2}-1{8}^{2}}$=24.
点评 此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
18. 如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )
如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )
 如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )
如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )| A. | 大于90° | B. | 等于90° | C. | 小于90° | D. | 无法确定 |
16.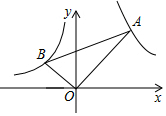 如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{2}{x}$,y=$\frac{8}{x}$的图象交于B、A两点,则tan∠OAB的值的变化趋势为:( )
如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{2}{x}$,y=$\frac{8}{x}$的图象交于B、A两点,则tan∠OAB的值的变化趋势为:( )
 如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{2}{x}$,y=$\frac{8}{x}$的图象交于B、A两点,则tan∠OAB的值的变化趋势为:( )
如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{2}{x}$,y=$\frac{8}{x}$的图象交于B、A两点,则tan∠OAB的值的变化趋势为:( )| A. | 逐渐变小 | B. | 逐渐变大 | C. | 时大时小 | D. | 保持不变 |
3. 如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( )
 如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论中不一定成立的是( )| A. | AB∥DC | B. | AC=BD | C. | AC⊥BD | D. | OA=OC |
17.2017年2月3日,据海关统计,2016年我国货物贸易进出口总值近24万亿元人民币,24万亿元用科学记数法表示为( )
| A. | 2.4×1013元 | B. | 240000×108元 | C. | 24×1012元 | D. | 24×108元 |
 如图,直线AC∥BD,P在直线AB上(不与点A,B重合).
如图,直线AC∥BD,P在直线AB上(不与点A,B重合).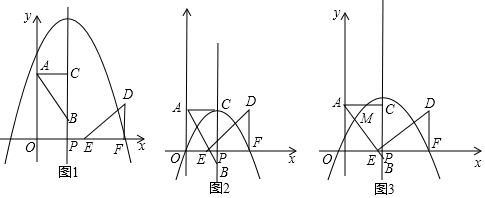
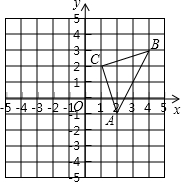 如图所示,△ABC的顶点都在平面直角坐标系的网格上.
如图所示,△ABC的顶点都在平面直角坐标系的网格上.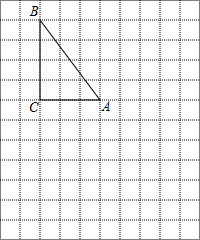 在右边网格图中,每个小正方形的边长均为1个单位长度,△ABC为直角三角形,∠C=90°,AC=3,BC=4.
在右边网格图中,每个小正方形的边长均为1个单位长度,△ABC为直角三角形,∠C=90°,AC=3,BC=4.