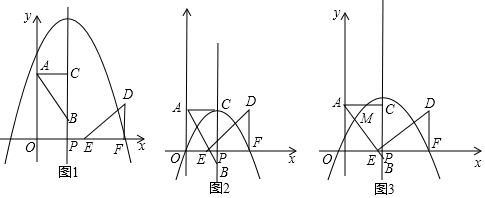
题目内容
1.已知:等边△ABC的边长为4,点P在线段AB上,点D在线段AC上,且△PDE为等边三角形,当点P与点B重合时(如图1),AD+AE的值为4;[类比探究]在上面的问题中,如果把点P沿BA方向移动,使PB=1,其余条件不变(如图2),AD+AE的值是多少?请写出你的计算过程;
[拓展迁移]如图3,△ABC中,AB=BC,∠ABC=a,点P在线段BA延长线上,点D在线段CA延长线上,在△PDE中,PD=PE,∠DPE=a,设AP=m,则线段AD、AE有怎样的等量关系?请用含m,a的式子直接写出你的结论.

分析 (1)只要证明△EPA≌△DPC,即可推出AE=CD,可得AD+AE=AD+DC=AC=4;
(2)[类比探究]:如图2中,作PK∥BC交AC于K.连接AE.利用(1)中的结论即可解决问题;
(3)[拓展迁移]:如图3中,作PJ⊥AD于J,在AD上取一点K,使得PK=PA.由△PDK≌△PEA,推出DK=AE,推出AD-AE=AK=2AJ=2•m•sin$\frac{α}{2}$即可解决问题;
解答 (1)解:如图1中,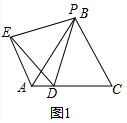
∵△PDE.△PAC都是等边三角形,
∴PE=PD,PA=PC,∠EPD=∠APC=60°,
∴∠EPA=∠DPC,
∴△EPA≌△DPC,
∴AE=CD,
∴AD+AE=AD+DC=AC=4.
(2)[类比探究]:解:AD+AE=3
理由:如图2中,作PK∥BC交AC于K.连接AE.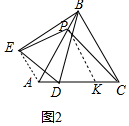
易证△PAK是等边三角形,
由上面题目可知.AE+AD=AK=3.
(3)[拓展迁移]:解:如图3中,作PJ⊥AD于J,在AD上取一点K,使得PK=PA.
易证∠APK=∠DPE=α,
∵PD=PE,PK=PA,
∴∠DPK=∠EPA,
∴△PDK≌△PEA,
∴DK=AE,
∴AD-AE=AK=2AJ=2•m•sin$\frac{α}{2}$.
∴AD-AE=2m•sin$\frac{α}{2}$.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质、锐角三角函数等知识,解题的关键正确寻找全等三角形解决问题,学会添加常用辅助线,构造全等三角形,学会用转化的思想思考问题,属于中考压轴题.

练习册系列答案
相关题目
11.若x=-3是方程kx-x+6=0的解,则k的值是( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
 把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=35°,则下面五个结论:①∠CEF=35°;②∠AEC=145°;③∠BGE=70°;④∠EFD′=110°;⑤∠D′FD=70°.其中正确的是①③⑤.(只填序号)
把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=35°,则下面五个结论:①∠CEF=35°;②∠AEC=145°;③∠BGE=70°;④∠EFD′=110°;⑤∠D′FD=70°.其中正确的是①③⑤.(只填序号) 在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点在网格线的交点处的三角形)ABC的顶点A、C的坐标系分别为A(-4,5)、C(-1,3).
在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点在网格线的交点处的三角形)ABC的顶点A、C的坐标系分别为A(-4,5)、C(-1,3). 如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{2}{x}$,y=$\frac{8}{x}$的图象交于B、A两点,则tan∠OAB的值的变化趋势为:( )
如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{2}{x}$,y=$\frac{8}{x}$的图象交于B、A两点,则tan∠OAB的值的变化趋势为:( )