题目内容
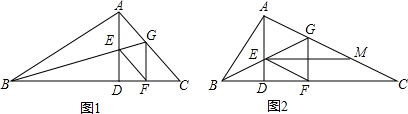
6.在△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC交AD于E,交AC于G,GF⊥BC于F,连接EF.(1)如图1,求证:四边形AEFG是菱形;
(2)如图2,若E为BG的中点,过点E作EM∥BC交AC于M,在不添加任何辅助线的情况下,请直接写出图2中是CM长$\sqrt{3}$倍的所有线段.
分析 (1)先证明四边形AEFG是平行四边形,再证明AE=AG即可.
(2)先证明AB=$\sqrt{3}$AG,再分别证明AB=BF=CF=EM,CM=AG即可.
解答 (1)证明:∵AD⊥BC,GF⊥BC,
∴∠ADF=∠GFC=90°,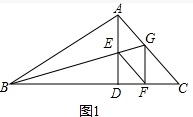
∴AE∥GF,
在△ABG和△FBG中,
$\left\{\begin{array}{l}{∠BAG=∠BFG}\\{∠ABG=∠FBG}\\{BG=BG}\end{array}\right.$,
∴△ABG≌△FBG,
∴AG=FG,
∵∠FBG+∠BED=90°,
∵∠BED=∠AEG,
∴∠FBG+∠AEG=90°,
∵∠ABG+∠AGE=90°,
∵∠ABG=∠FBG,
∴∠AEG=∠AGE,
∴AE=AG,
∴AE=FG,
∴四边形AEFG是平行四边形,
∵AE=AG∴四边形AEFG是菱形.
(2)解:∵四边形AEFG是菱形,
∴AE=AG,
∵BE=EG,∠BAG=90°,
∴AE=BE=EG,
∴△AEG是等边三角形,
∴∠AGE=60°,
在RT△ABG中,∵∠ABG=30°,
∴AB=$\sqrt{3}$AG,
∵∠C=30°,∴BC=2AB,
∴BE=GE,EF∥AC,EM∥BC,
∴BF=FC,CM=GM,
在RT△AEM中,∵∠AME=∠C=30°,∠GEM+∠GME=60°,
∴∠GEM=∠GME=30°,
∴EG=AG=GM=CM,
∵EM∥FC,EF∥CM,
∴四边形EFCM是平行四边形,
∴AB=BF=CF=EM=$\sqrt{3}$CM,
∴是CM长$\sqrt{3}$倍的所有线段有AB、BF、CF、EM.
点评 本题考查菱形的判定和性质、全等三角形的判定和性质、平行四边形的判定和性质、直角三角形30度角的性质等知识,寻找全等三角形是解题的关键,必须熟练掌握特殊三角形边角关系,属于中考常考题型.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案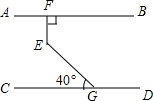 如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )
如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
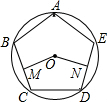 如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )
如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )| A. | 108° | B. | 144° | C. | 150° | D. | 166° |

 如图,已知梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,E是AB上一点,将△BCE沿着直线CE翻折,点B恰好与D点重合,则BE=$\frac{5}{2}$.
如图,已知梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,E是AB上一点,将△BCE沿着直线CE翻折,点B恰好与D点重合,则BE=$\frac{5}{2}$.