题目内容
15．
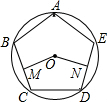如图，正五边形ABCDE内接于⊙O，点M为BC中点，点N为DE中点，则∠MON的大小为（ ）| A． | 108° | B． | 144° | C． | 150° | D． | 166° |
分析 由垂径定理得出∠OMC=∠OND=90°，由正五边形的性质得出∠C=∠D=108°，由五边形内角和即可求出结果．
解答 解：∵点M为BC中点，点N为DE中点，
∴OM⊥BC，ON⊥DE，
∴∠OMC=∠OND=90°，
∵五边形ABCDE是正五边形，
∴∠C=∠D=（5-2）×180°÷5=108°，
∴∠MON=（5-2）×180°-2×90°-2×108°=144°；
故选：B．
点评 本题考查了正五边形的性质、垂径定理；熟练掌握正五边形的性质，由垂径定理得出∠OMC=∠OND=90°是解决问题的关键．
练习册系列答案
相关题目
如图，AC是矩形ABCD的对角线，将矩形纸片折叠，使点C与点A重合，请在图中画出折痕，然后再在图中画出矩形ABCD的外接圆．（用尺规作图，写出结论，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔加黑）．
如图，在?ABCD中，AD=2AB，CM⊥AD，CN⊥AB，垂足分别为M、N，连接MN，ND．则下列结论一定正确的是①②③④．（请将序号在填在横线上）
（1）解不等式组$\left\{\begin{array}{l}{x≤3x+2}\\{x-1＜2-2x}\end{array}\right.$