题目内容
18.已知3a2-a-3=0,则$\frac{{a}^{2}}{{a}^{4}-{5a}^{2}+1}$=-$\frac{9}{26}$.分析 将3a2-a-3=0两边都除以a得a-$\frac{1}{a}$=$\frac{1}{3}$,原式分子分母都除以a2后再配方可得$\frac{1}{(a-\frac{1}{a})^{2}-3}$,把a-$\frac{1}{a}$=$\frac{1}{3}$代入可得答案.
解答 解:由3a2-a-3=0知a≠0,
将3a2-a-3=0两边都除以a得:3a-1-$\frac{3}{a}$=0,即3(a-$\frac{1}{a}$)=1,
可得:a-$\frac{1}{a}$=$\frac{1}{3}$,
故$\frac{{a}^{2}}{{a}^{4}-{5a}^{2}+1}$=$\frac{1}{{a}^{2}-5+\frac{1}{{a}^{2}}}$
=$\frac{1}{(a-\frac{1}{a})^{2}-3}$
=$\frac{1}{(\frac{1}{3})^{2}-3}$
=$-\frac{9}{26}$.
故答案为:-$\frac{9}{26}$.
点评 本题主要考查分式的化简求值能力,将原方程和待求分式根据等式基本性质和分式的性质通过变形得到包含a-$\frac{1}{a}$的式子是关键.

练习册系列答案
相关题目
8. 如图,在矩形ABCD中,AB=8,BC=4,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为( )
如图,在矩形ABCD中,AB=8,BC=4,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为( )
 如图,在矩形ABCD中,AB=8,BC=4,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为( )
如图,在矩形ABCD中,AB=8,BC=4,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为( )| A. | 6.4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 6 |
 如图,在△ABC中,∠B=45°,∠C=30°,AC=2,点D在BC上,将△ACD沿直线AD翻折后,点C落在点E处,边AE交边BC于点F,如果DE∥AB,那么$\frac{CF}{BF}$的值是$\sqrt{3}$+1.
如图,在△ABC中,∠B=45°,∠C=30°,AC=2,点D在BC上,将△ACD沿直线AD翻折后,点C落在点E处,边AE交边BC于点F,如果DE∥AB,那么$\frac{CF}{BF}$的值是$\sqrt{3}$+1.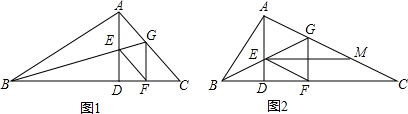
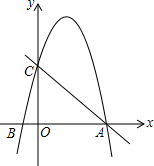 如图,平面直角坐标系xOy中,已知B(-1,0),一次函数y=-x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=-x2+bx+c的图象经过点A、点B.
如图,平面直角坐标系xOy中,已知B(-1,0),一次函数y=-x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=-x2+bx+c的图象经过点A、点B.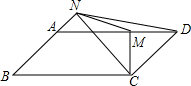 如图,在?ABCD中,AD=2AB,CM⊥AD,CN⊥AB,垂足分别为M、N,连接MN,ND.则下列结论一定正确的是①②③④.(请将序号在填在横线上)
如图,在?ABCD中,AD=2AB,CM⊥AD,CN⊥AB,垂足分别为M、N,连接MN,ND.则下列结论一定正确的是①②③④.(请将序号在填在横线上)