题目内容
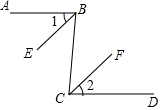
20. 如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.
如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.
分析 由AB∥CD,利用两直线平行同位角相等得到一对角相等,再由已知角相等,利用等式的性质得到一对同位角相等,可得出EP∥FQ.
解答 证明:∵AB∥CD,
∴∠MEB=∠MFD.
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,即∠MEP=∠MFQ,
∴EP∥FQ.
点评 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
5.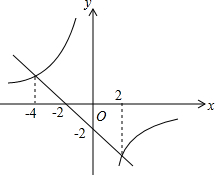 若一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象如图所示,则关于x的不等式kx+b-$\frac{m}{x}$≤-2的解集为( )
若一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象如图所示,则关于x的不等式kx+b-$\frac{m}{x}$≤-2的解集为( )
 若一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象如图所示,则关于x的不等式kx+b-$\frac{m}{x}$≤-2的解集为( )
若一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象如图所示,则关于x的不等式kx+b-$\frac{m}{x}$≤-2的解集为( )| A. | 0<x≤2或x≤-4 | B. | -4≤x<0或x≥2 | C. | $-2\sqrt{2}$≤x<0或x$≥2\sqrt{2}$ | D. | x$≤-2\sqrt{2}$或0$<x≤2\sqrt{2}$ |
9.抽查的甲、乙两班部分学生的视力,记录如下:
(1)求两组数据的平均数,众数,中位数.
(2)比较两组数据的特征,谈谈对“极端值”的认识.
| 甲班 | 0.1 | 0.9 | 1.0 | 1.1 | 1.1 | 1.3 | 1.5 |
| 乙班 | 0.8 | 0.9 | 1.0 | 1.1 | 1.1 | 1.3 | 1.5 |
(2)比较两组数据的特征,谈谈对“极端值”的认识.
 填写下面证明过程中的推理依据:
填写下面证明过程中的推理依据: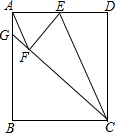 如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF.
如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF.