题目内容
2.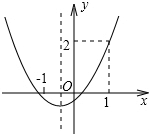 已知抛物线y=ax2+bx+c的图象如图所示,则下列结论中正确是( )
已知抛物线y=ax2+bx+c的图象如图所示,则下列结论中正确是( )| A. | a+b+c>2 | B. | 2a-b<0 | C. | b<1 | D. | 3a+c>2 |
分析 利用x=1时,函数值为2可对A进行判断;利用对称轴的位置得到1<-$\frac{b}{2a}$<0,再根据不等式的性质可对B进行判断;利用x=-1时函数值为负数得到a-b+c<0,再利用a+c=2-b可对C进行判断;利用2a>b和a+b+c=2可对D进行判断.
解答 解:A、因为抛物线过点(1,2),则a+b+c=2,所以A选项错误;
B、因为-1<-$\frac{b}{2a}$<0,而a>0,所以2a-b>0,所以B选项错误;
C、因为x=-1时,y<0,即a-b+c<0,而a+c=2-b,则2-b-b<0,即b>1,所以B选项错误;
D、因为2a>b,所以3a+c=a+2a+c>a+b+c,所以3a+c>2,所以D选项正确.
故选D.
点评 本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.判断C、D的关键是利用a+b+c=2和不等式2a>b进行变形.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
12.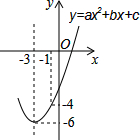 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
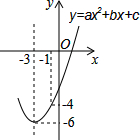 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )| A. | b2>4ac | |
| B. | ax2+bx+c≥-6 | |
| C. | 关于x的一元二次方程ax2+bx+c=-4的两根分别为-5和-1 | |
| D. | 若点(-2,m),(-5,n)在抛物线上,则m>n |
10.对于两个不相等的实数a、b,我们规定符号max{a,b}表示a、b中较大的数,如:max{2,4}=4.按照这个规定.方程max{x,-x}=$\frac{2x+1}{x}$的解为( )
| A. | $1-\sqrt{2}$ | B. | $2-\sqrt{2}$ | C. | $1-\sqrt{2}$或$1+\sqrt{2}$ | D. | $1+\sqrt{2}$或-1 |
7.济宁市某经济开发区,今年一月份工业产值达10亿元,第一季度总产值为75亿元,二、三月平均每月增长率是多少,若设平均每月的增长率为x,根据题意,可列方程为( )
| A. | 10(1+x)2=75 | B. | 10+10(1+x)+10(1+x)2=75 | ||
| C. | 10(1+x)+10(1+x)2=75 | D. | 10+10(1+x)2=75 |
11.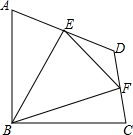 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )| A. | 2 | B. | $\frac{9}{4}$ | C. | $\frac{5}{2}$ | D. | 3 |
12.已知点P(a,b)在反比例函数y=-$\frac{6}{x}$的图象上,则ab的值为( )
| A. | 6 | B. | $\frac{1}{6}$ | C. | -6 | D. | -$\frac{1}{6}$ |
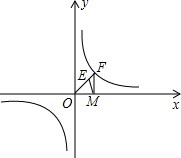 已知:反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(1,1)
已知:反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(1,1)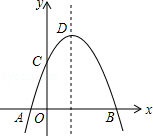 如图,抛物线y=-x2+2x+m+1交x轴与点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
如图,抛物线y=-x2+2x+m+1交x轴与点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题: