��Ŀ����
13��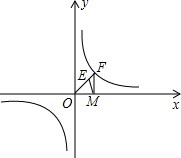 ��֪������������y=$\frac{k}{x}$��k��0����ͼ����B��1��1��
��֪������������y=$\frac{k}{x}$��k��0����ͼ����B��1��1����1����÷�������������ʽ��
��2������OB���ٰѵ�A��2��0�����B���ӣ�����OAB�Ƶ�O��˳ʱ�뷽����ת135��õ���OA��B�䣬д��A��B����е�P�����꣬���жϵ�P�Ƿ��ڴ�˫�����ϣ���˵�����ɣ�
��3����ͼ�����÷���������ͼ������һ��F��2m��m-$\frac{1}{2}$��������m��0����������OF����ȡһ��E����E���������Ϊn����F����FM��x���ڵ�M������EM��ʹ��OEM�������$\frac{\sqrt{2}}{2}$����n��ֵ��
���� ��1����B��1��1������y=$\frac{k}{x}$���ɵõ����ۣ�
��2��������ת�����ʵõ���AOA��=135�㣬OA��=OA���������Ǻ����Ķ���õ�A�䣨-$\sqrt{2}$��-$\sqrt{2}$����B�䣨0��-$\sqrt{2}$�������ǵõ����ۣ�
��3����F��2m��m-$\frac{1}{2}$������y=$\frac{1}{x}$���õ�m1=1��m2=-$\frac{1}{2}$������S��OEM=$\frac{\sqrt{2}}{2}$�����n=$\frac{\sqrt{2}}{2}$��
���  �⣺��1����B��1��1����y=$\frac{k}{x}$��ͼ���ϣ�
�⣺��1����B��1��1����y=$\frac{k}{x}$��ͼ���ϣ�
��k=xy=1��1=1��
��y=$\frac{1}{x}$��
��2����ͼ1����A��2��0����B��1��1����
��OA=2��OB=$\sqrt{2}$��
�߽���OAB�Ƶ�O��˳ʱ�뷽����ת135��õ���OA��B�䣬
���AOA��=135�㣬OA��=OA��
��A�䣨-$\sqrt{2}$��-$\sqrt{2}$����B�䣨0��-$\sqrt{2}$����
��A��B����е�ΪP��-$\frac{\sqrt{2}}{2}$��-$\sqrt{2}$����
�ߣ�-$\frac{\sqrt{2}}{2}$������-$\sqrt{2}$��=1��
��P��˫�����ϣ�
��3����ͼ2����F��2m��m-$\frac{1}{2}$���ڷ���������y=$\frac{1}{x}$ͼ���ϣ�
��m1=1��m2=-$\frac{1}{2}$��
�֡�m=1��
��F��2��$\frac{1}{2}$����
��FM��x�ᣬ
��m��2��0������M��2��0������OM=2��
��S��OEM=$\frac{\sqrt{2}}{2}$��
��$\frac{1}{2}$OM•n=$\frac{\sqrt{2}}{2}$����$\frac{1}{2}$��2n=$\frac{\sqrt{2}}{2}$��
��n=$\frac{\sqrt{2}}{2}$��
���� ���⿼�����ô���ϵ�������������Ľ���ʽ����ת�����ʣ�����������ļ��㣬������Ǻ������ó�A�䣨-$\sqrt{2}$��-$\sqrt{2}$����B�䣨0��-$\sqrt{2}$���ǽ���Ĺؼ���


| A�� | 56 | B�� | 63 | C�� | 70 | D�� | 77 |
| A�� | $\sqrt{3}$ | B�� | $\sqrt{2}$ | C�� | 1 | D�� | 0 |
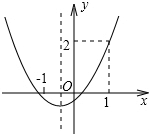 ��֪������y=ax2+bx+c��ͼ����ͼ��ʾ�������н�������ȷ�ǣ�������
��֪������y=ax2+bx+c��ͼ����ͼ��ʾ�������н�������ȷ�ǣ�������| A�� | a+b+c��2 | B�� | 2a-b��0 | C�� | b��1 | D�� | 3a+c��2 |
 �ס��������ﳵ�ֱ��A��B����ͬʱ������������У����˴ӳ���������������6Сʱ�����������ڴ˹����У����ı���һ���ﳵ�ٶȣ�����������ʻ·��y��km������ʻʱ��x��ʱ��֮��ĺ���ͼ��ֱ�Ϊ����OA-AB������OC-CD����ͼ��ʾ��
�ס��������ﳵ�ֱ��A��B����ͬʱ������������У����˴ӳ���������������6Сʱ�����������ڴ˹����У����ı���һ���ﳵ�ٶȣ�����������ʻ·��y��km������ʻʱ��x��ʱ��֮��ĺ���ͼ��ֱ�Ϊ����OA-AB������OC-CD����ͼ��ʾ��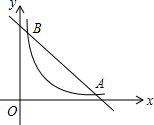 ��ͼ����ֱ������ϵ�У�ֱ��y=6-x��˫����$y=\frac{4}{x}$ ��x��0����ͼ���ཻ��A��B�����A������Ϊ��m��n������ô��mΪ����nΪ���ľ��ε�������ܳ��ֱ�Ϊ4��12��
��ͼ����ֱ������ϵ�У�ֱ��y=6-x��˫����$y=\frac{4}{x}$ ��x��0����ͼ���ཻ��A��B�����A������Ϊ��m��n������ô��mΪ����nΪ���ľ��ε�������ܳ��ֱ�Ϊ4��12��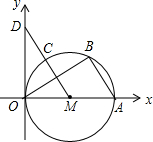 ��ͼ��ֱ��ΪOA��ԲM��x�ύ�ڵ�O��A����B��C�Ѱ�ԲOA��Ϊ���ȷݣ�����MC���ӳ���y���ڵ�D��
��ͼ��ֱ��ΪOA��ԲM��x�ύ�ڵ�O��A����B��C�Ѱ�ԲOA��Ϊ���ȷݣ�����MC���ӳ���y���ڵ�D��
