题目内容
如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与CD的位置关系,并说明理由;
(2)如图2,∠AEF与∠EFC的角平分线交于点P,PF∥GH,求证:GH⊥EG;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.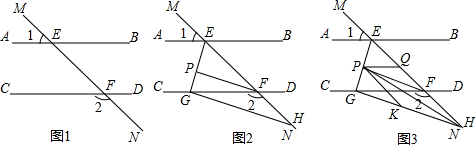
(1)试判断直线AB与CD的位置关系,并说明理由;
(2)如图2,∠AEF与∠EFC的角平分线交于点P,PF∥GH,求证:GH⊥EG;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

考点:平行线的判定与性质
专题:
分析:(1)证明∠AEF=∠2,得到AB∥CD.
(2)证明PF⊥GE,此为解题的关键性结论;由PF∥GH,得到GH⊥EG.
(3)证明∠FPH=∠KPH(设为α);证明∠KPQ=45°+α,此为解题的关键性结论;即可解决问题.
(2)证明PF⊥GE,此为解题的关键性结论;由PF∥GH,得到GH⊥EG.
(3)证明∠FPH=∠KPH(设为α);证明∠KPQ=45°+α,此为解题的关键性结论;即可解决问题.
解答: 解:(1)∵∠1+∠AEF=180°,
解:(1)∵∠1+∠AEF=180°,
∠1+∠2=180°,
∴∠AEF=∠2,
∴AB∥CD.
(2)∵AB∥CD,
∴∠AEF+∠EFC=180°;
∵∠AEF与∠EFC的角平分线交于点P,
∴∠PEF+∠PFE=90°,即PF⊥GE;
∵PF∥GH,
∴GH⊥EG.
(3)∵PF∥GH,
∴∠FPH=∠PHK,而∠PHK=∠HPK,
∴∠FPH=∠KPH(设为α);
∵PQ平分∠EPK,
∴∠KPQ=
=45°+α,
∴∠HPQ=45°+α-α=45°,
即∠HPQ的大小不会发生变化.
 解:(1)∵∠1+∠AEF=180°,
解:(1)∵∠1+∠AEF=180°,∠1+∠2=180°,
∴∠AEF=∠2,
∴AB∥CD.
(2)∵AB∥CD,
∴∠AEF+∠EFC=180°;
∵∠AEF与∠EFC的角平分线交于点P,
∴∠PEF+∠PFE=90°,即PF⊥GE;
∵PF∥GH,
∴GH⊥EG.
(3)∵PF∥GH,
∴∠FPH=∠PHK,而∠PHK=∠HPK,
∴∠FPH=∠KPH(设为α);
∵PQ平分∠EPK,
∴∠KPQ=
| 90°+2α |
| 2 |
∴∠HPQ=45°+α-α=45°,
即∠HPQ的大小不会发生变化.
点评:该题主要考查了平行线的性质及其应用问题;解题的关键是牢固掌握定理内容,灵活运用定理来分析、判断、解答.

练习册系列答案
相关题目
当x=1时,代数式ax3+bx+1的值为2014;则当x=-1时,ax3+bx+1的值为( )
| A、2012 | B、2015 |
| C、-2012 | D、不能确定 |
 如图,在四边形ABCD中,∠BAD=∠BCD=90°,AC平分∠BCD.若BC=7,AC=4
如图,在四边形ABCD中,∠BAD=∠BCD=90°,AC平分∠BCD.若BC=7,AC=4 如图,一次函数y=kx+3与反例函数y=
如图,一次函数y=kx+3与反例函数y= 如图,△ABC≌△DEF,点F在BC边上,AB与EF相交于点P.若∠DEF=37°,PB=PF,则∠APF=
如图,△ABC≌△DEF,点F在BC边上,AB与EF相交于点P.若∠DEF=37°,PB=PF,则∠APF=