题目内容
 如图,在四边形ABCD中,∠BAD=∠BCD=90°,AC平分∠BCD.若BC=7,AC=4
如图,在四边形ABCD中,∠BAD=∠BCD=90°,AC平分∠BCD.若BC=7,AC=4| 2 |
考点:全等三角形的判定与性质,角平分线的性质
专题:
分析:过A作AN⊥BC于N,AM⊥CD于M,根据角平分线性质和已知求出AM=AN,∠M=∠ANB=90°,∠1=∠2=45°,求出∠ABN=∠3,根据AAS推出△ANB≌△AMD,根据全等得出BN=DM,根据SAS推出△AMC≌△ANC,根据全等得出CM=CN,求出AM=MC=4,求出BN,即可得出答案.
解答:解:过A作AN⊥BC于N,AM⊥CD于M,
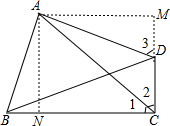
∵AC平分∠BCD,∠BCD=90°,
∴AM=AN,∠M=∠ANB=90°,∠1=∠2=45°
∵∠BAD=∠BCD=90°,
∴∠ABN+∠ADC=360°-90°-90°=180°,
∵∠3+∠ADC=180°,
∴∠ABN=∠3,
在△ANB和△AMD中
∴△ANB≌△AMD,
∴BN=DM,
在△AMC和△ANC中,
,
∴△AMC≌△ANC(AAS),
∴CM=CN,
∵在Rt△AMC中,∠M=90°,∠2=45°,AC=4
,
∴AM=MC=4,
∴CN=CM=4,
∵BC=7,
∴BN=7-4=3,
∴CD=CM-DM=4-3=1,
故答案为:1.

∵AC平分∠BCD,∠BCD=90°,
∴AM=AN,∠M=∠ANB=90°,∠1=∠2=45°
∵∠BAD=∠BCD=90°,
∴∠ABN+∠ADC=360°-90°-90°=180°,
∵∠3+∠ADC=180°,
∴∠ABN=∠3,
在△ANB和△AMD中
|
∴△ANB≌△AMD,
∴BN=DM,
在△AMC和△ANC中,
|
∴△AMC≌△ANC(AAS),
∴CM=CN,
∵在Rt△AMC中,∠M=90°,∠2=45°,AC=4
| 2 |
∴AM=MC=4,
∴CN=CM=4,
∵BC=7,
∴BN=7-4=3,
∴CD=CM-DM=4-3=1,
故答案为:1.
点评:本题考查了全等三角形的性质和判定,角平分线性质,勾股定理等知识点的应用,解此题的关键是求出CN=CM,BN=DM和求出各个线段的长.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
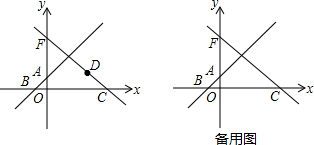 在平面直角坐标系xOy中,直线AB与直线y=-
在平面直角坐标系xOy中,直线AB与直线y=-