题目内容
【问题提出】已知∠AOB=70°,∠AOD=
∠AOC,∠BOD=3∠BOC(∠BOC<45°),求∠BOC的度数.
【问题思考】聪明的小明用分类讨论的方法解决.
(1)当射线OC在∠AOB的内部时,①若射线OD在∠AOC内部,如图1,可求∠BOC的度数,解答过程如下:
问:当射线OC在∠AOB的内部时,②若射线OD在∠AOB外部,如图2,请你求出∠BOC的度数;
【问题延伸】(2)当射线OC在∠AOB的外部时,请你画出图形,并求∠BOC的度数.
【问题解决】综上所述:∠BOC的度数分别是 .

| 1 |
| 2 |
【问题思考】聪明的小明用分类讨论的方法解决.
(1)当射线OC在∠AOB的内部时,①若射线OD在∠AOC内部,如图1,可求∠BOC的度数,解答过程如下:
设∠BOC=α,∴∠BOD=3∠BOC=3α,∴∠COD=∠BOD-∠BOC=2α,∴∠AOD=
∴∠AOD=∠COD=2α,∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,∴α=14°,∴∠BOC=14° |
【问题延伸】(2)当射线OC在∠AOB的外部时,请你画出图形,并求∠BOC的度数.
【问题解决】综上所述:∠BOC的度数分别是

考点:角的计算
专题:分类讨论
分析:(1)②由已知条件得出∠COD、∠AOD、∠AOB与∠BOC的关系,求出∠BOC的度数;
(2)分类讨论,根据∠AOD、∠BOD.∠AOB与∠BOC的关系,得出∠BOC的度数.
(2)分类讨论,根据∠AOD、∠BOD.∠AOB与∠BOC的关系,得出∠BOC的度数.
解答: 解:(1)②设∠BOC=α,则∠BOD=3α,②若射线OD在∠AOB外部,
解:(1)②设∠BOC=α,则∠BOD=3α,②若射线OD在∠AOB外部,
如图2:∠COD=∠BOD-∠BOC=2α,
∵∠AOD=
∠AOC,
∴∠AOD=
∠COD=
α,
∴∠AOB=∠BOD-∠AOD=3α-
α=
α=70°,
∴α=30°.
∴∠BOC=30°;
 (2)当射线OC在∠AOB外部时,根据题意,此时射线OC靠近射线OB,
(2)当射线OC在∠AOB外部时,根据题意,此时射线OC靠近射线OB,
∵∠BOC<45°,∠AOD=
∠AOC,
∴射线OD的位置也只有两种可能;
①若射线OD在∠AOB内部,如图3所示,
则∠COD=∠BOC+∠COD=4α,
∴∠AOB=∠BOD+∠AOD=3α+4α=7α=70°,
∴α=10°,
 ∴∠BOC=10°;
∴∠BOC=10°;
②若射线OD在∠AOB外部,如图4,
则∠COD=∠BOC+∠BOD=4α,
∵∠AOD=
∠AOC,
∴∠AOD=
∠COD=
α,
∴∠AOB=∠BOD-∠AOD=3α-
α=
α=70°,
∴α=42°,
∴∠BOC=42°;
综上所述:∠BOC的度数分别是14°,30°,10°,42°.
 解:(1)②设∠BOC=α,则∠BOD=3α,②若射线OD在∠AOB外部,
解:(1)②设∠BOC=α,则∠BOD=3α,②若射线OD在∠AOB外部,如图2:∠COD=∠BOD-∠BOC=2α,
∵∠AOD=
| 1 |
| 2 |
∴∠AOD=
| 1 |
| 3 |
| 2 |
| 3 |
∴∠AOB=∠BOD-∠AOD=3α-
| 2 |
| 3 |
| 7 |
| 3 |
∴α=30°.
∴∠BOC=30°;
 (2)当射线OC在∠AOB外部时,根据题意,此时射线OC靠近射线OB,
(2)当射线OC在∠AOB外部时,根据题意,此时射线OC靠近射线OB,∵∠BOC<45°,∠AOD=
| 1 |
| 2 |
∴射线OD的位置也只有两种可能;
①若射线OD在∠AOB内部,如图3所示,
则∠COD=∠BOC+∠COD=4α,
∴∠AOB=∠BOD+∠AOD=3α+4α=7α=70°,
∴α=10°,
 ∴∠BOC=10°;
∴∠BOC=10°;②若射线OD在∠AOB外部,如图4,
则∠COD=∠BOC+∠BOD=4α,
∵∠AOD=
| 1 |
| 2 |
∴∠AOD=
| 1 |
| 3 |
| 4 |
| 3 |
∴∠AOB=∠BOD-∠AOD=3α-
| 4 |
| 3 |
| 5 |
| 3 |
∴α=42°,
∴∠BOC=42°;
综上所述:∠BOC的度数分别是14°,30°,10°,42°.
点评:根据OC、OD的不同位置分类讨论∠BOC的计算方法;分类讨论是关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
2.6万是精确到( )
| A、百分位 | B、千位 |
| C、十分位 | D、百位 |
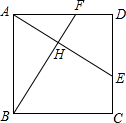 如图,在正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点H
如图,在正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点H(1)判断线段AE,BF的位置关系,并说明理由;
(2)找出图中所有与△ABH相似的三角形.(不添加任何辅助线)
 如图,这个图形旋转一周会与原图形重合几次?( )
如图,这个图形旋转一周会与原图形重合几次?( )| A、0 | B、1 | C、2 | D、4 |
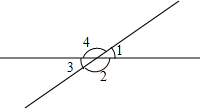 如图,已知∠2比∠1大90°,求∠1,∠3,∠4的度数.
如图,已知∠2比∠1大90°,求∠1,∠3,∠4的度数.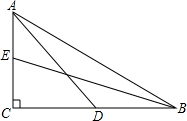 如图,Rt△ABC中,∠C=90°,AD、BE为Rt△ABC的两条中线,AD=6,BE=8,则AB=
如图,Rt△ABC中,∠C=90°,AD、BE为Rt△ABC的两条中线,AD=6,BE=8,则AB= 如图,将A向右移20个单位长度,再向左移15个单位长度,那么该点表示的数是
如图,将A向右移20个单位长度,再向左移15个单位长度,那么该点表示的数是 三条直线AB,CD,EF,如果AB∥EF,CD∥EF,想一想直线AB与CD可能相交吗?为什么?
三条直线AB,CD,EF,如果AB∥EF,CD∥EF,想一想直线AB与CD可能相交吗?为什么?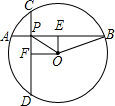 如图,在⊙O中,弦AB=CD,AB⊥CD,垂足为P,OE⊥AB于E,OF⊥CD于F,
如图,在⊙O中,弦AB=CD,AB⊥CD,垂足为P,OE⊥AB于E,OF⊥CD于F,