题目内容
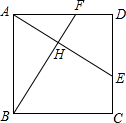 如图,在正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点H
如图,在正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点H(1)判断线段AE,BF的位置关系,并说明理由;
(2)找出图中所有与△ABH相似的三角形.(不添加任何辅助线)
考点:正方形的性质,全等三角形的判定与性质,相似三角形的判定
专题:
分析:(1)根据正方形的性质得出∠BAF=∠D=90°,AB=AD=DC,求出DE=AF,根据SAS推出△BAF≌△ADE,根据全等得出∠ABF=∠DAE,求出∠AHB=90°即可;
(2)图中所有与△ABH相似的三角形是△FBA和△EAD,根据相似三角形的判定推出△ABH∽△FBA和△FBA≌△EAD即可.
(2)图中所有与△ABH相似的三角形是△FBA和△EAD,根据相似三角形的判定推出△ABH∽△FBA和△FBA≌△EAD即可.
解答:解:(1)AE⊥BF,
理由是:∵四边形ABCD是正方形,
∴∠BAF=∠D=90°,AB=AD=DC,
∵CE=DF,
∴DE=AF,
在△BAF和△ADE中,
,
∴△BAF≌△ADE(SAS),
∴∠ABF=∠DAE,
∵∠BAF=90°,
∴∠DAE+∠BAH=90°,
∴∠ABF+∠BAH=90°,
∴∠AHB=180°-90°=90°,
∴AE⊥BF;
(2)图中所有与△ABH相似的三角形是△FBA和△EAD,
理由是:∵∠ABH=∠ABF,∠AHB=∠BAF=90°,
∴△ABH∽△FBA,
∵△FBA≌△EAD,
∴△ABH∽△EAD.
理由是:∵四边形ABCD是正方形,
∴∠BAF=∠D=90°,AB=AD=DC,
∵CE=DF,
∴DE=AF,
在△BAF和△ADE中,
|
∴△BAF≌△ADE(SAS),
∴∠ABF=∠DAE,
∵∠BAF=90°,
∴∠DAE+∠BAH=90°,
∴∠ABF+∠BAH=90°,
∴∠AHB=180°-90°=90°,
∴AE⊥BF;
(2)图中所有与△ABH相似的三角形是△FBA和△EAD,
理由是:∵∠ABH=∠ABF,∠AHB=∠BAF=90°,
∴△ABH∽△FBA,
∵△FBA≌△EAD,
∴△ABH∽△EAD.
点评:本题考查了正方形的性质,全等三角形的性质和判定,三角形的内角和定理,相似三角形的判定的应用,解此题的关键是求出△ABH∽△FBA,△FBA≌△EAD,综合性比较强,难度适中.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 如图,在△ABC中,若DE∥BC,
如图,在△ABC中,若DE∥BC,| AD |
| AB |
| 1 |
| 2 |
| A、8cm | B、12cm |
| C、11cm | D、10cm |
 如图,下列结论中,正确的是( )
如图,下列结论中,正确的是( )| A、∠DAC与∠ACB是一对同位角 |
| B、若∠DAC=∠ACB,则AB∥CD |
| C、∠D与∠DAC是一对同旁内角 |
| D、若∠D=∠B,则AD∥BC |
下列无理数中,在-4与-3之间的是( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于E,交BC于D.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于E,交BC于D. 如图,在Rt△ABC中,∠ACB=Rt∠,AC=2BC=2,作内接正方形A1B1D1C;在Rt△AA1B1中,作内接正方形A2B2D2A1;在Rt△AA2B2中,作内接正方形A3B3D3A2;…;依次作下去,则第1个正方形A1B1D1C的边长是
如图,在Rt△ABC中,∠ACB=Rt∠,AC=2BC=2,作内接正方形A1B1D1C;在Rt△AA1B1中,作内接正方形A2B2D2A1;在Rt△AA2B2中,作内接正方形A3B3D3A2;…;依次作下去,则第1个正方形A1B1D1C的边长是
 如图,已知点A,B的坐标分别为A(5.5,12),B(10.5,0),若P是y轴上一动点,求△ABP周长的最小值.
如图,已知点A,B的坐标分别为A(5.5,12),B(10.5,0),若P是y轴上一动点,求△ABP周长的最小值. 如图,BD⊥AC,CE⊥AB,垂足分别为点D和点E,BD与CE相交于点F,BF=CF.求证:点F在∠BAC的平分线上.
如图,BD⊥AC,CE⊥AB,垂足分别为点D和点E,BD与CE相交于点F,BF=CF.求证:点F在∠BAC的平分线上.