题目内容
13.若2m=3,2n=4,则23m-2n等于( )| A. | $\frac{27}{16}$ | B. | $\frac{27}{8}$ | C. | $\frac{9}{8}$ | D. | 11 |
分析 直接利用同底数米的除法运算法则结合幂的乘方运算法则将原式变形求出答案.
解答 解:∵2m=3,2n=4,
∴23m-2n
=23m÷22n
=(2m)3÷(2n)2
=33÷42
=$\frac{27}{16}$.
故选:A.
点评 此题主要考查了同底数幂的除法运算、幂的乘方运算,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
4.已知点P在第四象限,且到x轴的距离是2,到y轴的距离是3,则点P的坐标为( )
| A. | (2,-3) | B. | (-3,2) | C. | (3,-2) | D. | (-2,3) |
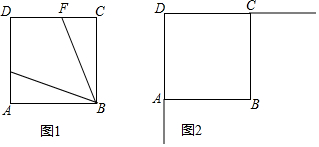
1. 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )
 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{6}$ |
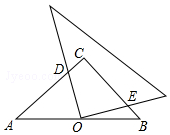
18. 如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )
如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )
 如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )
如图所示,把一长方形纸片沿MN折叠后,点D,C分别落在D′,C′的位置.若∠AMD′=35°,则∠NFD′等于( )| A. | 115° | B. | 125° | C. | 135° | D. | 145° |
5.若-4≤x≤3,化简$\sqrt{{x}^{2}+8x+16}$-$\sqrt{{x}^{2}-6x+9}$的结果为( )
| A. | 2x+1 | B. | -2x-1 | C. | 1 | D. | 7 |
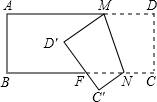
2. 一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( )
一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( )
 一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( )
一张矩形纸片ABCD,AD=5cm,AB=3cm,将纸片沿ED折叠,A点刚好落在BC边上的A'处,如图,这时AE的长应该是( )| A. | $\frac{5}{3}$cm | B. | $\frac{4}{3}$cm | C. | $\frac{3}{2}$cm | D. | $\frac{7}{5}$cm |
3. 如图,菱形ABCD的对角线AC,BD相交于点O,AC=8cm,BD=6cm,AC上一动点P从点C出发,沿CA方向以1cm/s的速度向A运动,设点P运动时间为ts.当t等于( )时,△PCD是直角三角形.
如图,菱形ABCD的对角线AC,BD相交于点O,AC=8cm,BD=6cm,AC上一动点P从点C出发,沿CA方向以1cm/s的速度向A运动,设点P运动时间为ts.当t等于( )时,△PCD是直角三角形.
 如图,菱形ABCD的对角线AC,BD相交于点O,AC=8cm,BD=6cm,AC上一动点P从点C出发,沿CA方向以1cm/s的速度向A运动,设点P运动时间为ts.当t等于( )时,△PCD是直角三角形.
如图,菱形ABCD的对角线AC,BD相交于点O,AC=8cm,BD=6cm,AC上一动点P从点C出发,沿CA方向以1cm/s的速度向A运动,设点P运动时间为ts.当t等于( )时,△PCD是直角三角形.| A. | $\frac{9}{4}$s | B. | 4s | C. | $\frac{9}{4}$s或$\frac{25}{4}$s | D. | 4s或$\frac{25}{4}$s |