题目内容
1.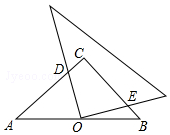 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )
如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=$\sqrt{6}$,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AB、BC相交,交点分别为D、E,则CD+CE=( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{6}$ |
分析 连接CO,可证明△COD≌△BOE,可证得CD=BE,可得CD+CE=BC,利用勾股定理可求得BC的长,则可求得答案.
解答 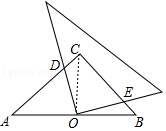 解:
解:
如图,连接CO,
由题意可知AB=BC,且O为AB的中点,
∴CO=BO,∠DCO=∠EBO=45°,
∵∠DOE=∠COB=90°,
∴∠COD+∠COE=∠COE+∠BOE=90°,
∴∠COD=∠BOE,
在△COD和△BOE中
$\left\{\begin{array}{l}{∠COD=∠BOE}\\{CO=BO}\\{∠DCO=∠EBO}\end{array}\right.$
∴△COD≌△BOE(ASA),
∴CD=BE,
∴CE+CD=CE+BE=BC,
在Rt△ABC中,AB=$\sqrt{6}$,
∴BC=$\frac{\sqrt{6}}{\sqrt{2}}$=$\sqrt{3}$,
∴CD+CE=$\sqrt{3}$,
故选A.
点评 本题主要考查全等三角形的判定和性质及等腰直角三角形的性质,证得△COD≌△BOE,把CD+CE转化为BC的长是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.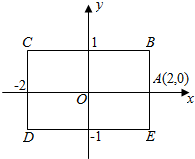 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是( )
 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是( )| A. | (2,0) | B. | (-1,1) | C. | (-2,1) | D. | (-1,-1) |
12.如果式子$\sqrt{a-1}$是二次根式,那么a的取值范围是( )
| A. | a≥1 | B. | a>1 | C. | a=1 | D. | a≤1 |
9.若64x2+axy+y2是一个完全平方式,那么a的值应该是( )
| A. | 8 | B. | 16 | C. | -16 | D. | 16或-16 |
16.计算结果为x2+7x-18的是( )
| A. | (x+2)(x-9) | B. | (x-2)(x+9) | C. | (x+3)(x+9) | D. | (x-3)(x+6) |
6.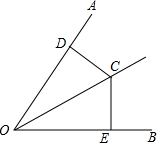 如图,OC是∠AOB的角平分线.D,E分别是OA,OB上的点,则下列条件中不能判定△OCD与△OCE全等的是( )
如图,OC是∠AOB的角平分线.D,E分别是OA,OB上的点,则下列条件中不能判定△OCD与△OCE全等的是( )
 如图,OC是∠AOB的角平分线.D,E分别是OA,OB上的点,则下列条件中不能判定△OCD与△OCE全等的是( )
如图,OC是∠AOB的角平分线.D,E分别是OA,OB上的点,则下列条件中不能判定△OCD与△OCE全等的是( )| A. | ∠OCD=∠OCE | B. | CD⊥OA,CE⊥OB | C. | OD=OE | D. | CD=CE |
13.若2m=3,2n=4,则23m-2n等于( )
| A. | $\frac{27}{16}$ | B. | $\frac{27}{8}$ | C. | $\frac{9}{8}$ | D. | 11 |
10.在函数y=$\frac{\sqrt{3x+6}}{x}$中,自变量x的取值范围是( )
| A. | x≥-2 | B. | x>-0 | C. | x≥-2且x≠0 | D. | x>-2且x≠0 |
11. 如图,将一张矩形的纸对折,旋转90°后再对折,然后沿着右图中的虚线剪下,则剪下的纸片打开后的形状一定为( )
如图,将一张矩形的纸对折,旋转90°后再对折,然后沿着右图中的虚线剪下,则剪下的纸片打开后的形状一定为( )
 如图,将一张矩形的纸对折,旋转90°后再对折,然后沿着右图中的虚线剪下,则剪下的纸片打开后的形状一定为( )
如图,将一张矩形的纸对折,旋转90°后再对折,然后沿着右图中的虚线剪下,则剪下的纸片打开后的形状一定为( )| A. | 三角形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |