题目内容
19.在等腰△ABC中,D为线段BC上一点,AD⊥BC,若AB=5,AD=3,CD=4或1.分析 分三种情况:①当AB=AC=5时,如图1,②当AB=BC=5时,如图2,③当AC=BC时,如图3,分别根据勾股定理和等腰三角形的性质求CD的长即可.
解答  解:分三种情况:
解:分三种情况:
①当AB=AC=5时,如图1,
∵AD⊥BC,
∴∠ADC=90°,BD=DC,
在Rt△ADC中,由勾股定理得:DC=$\sqrt{{5}^{2}-{3}^{2}}$=4,
②当AB=BC=5时,如图2,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
同理得:BD=4,
∴DC=5-4=1,
③当AC=BC时,如图3,
同理得:BD=4,
设CD=x,则AC=x+4,
由勾股定理得:(x+4)2=x2+32,
8x=-7,
x=-$\frac{7}{8}$(不符合题意,舍),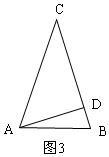
综上所述,DC的长为4或1;
故答案为:4或1.
点评 本题考查了等腰三角形的定义、勾股定理,根据已知不确定腰的情况下,分三种情况进行讨论解决问题,并与勾股定理相结合解题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
9.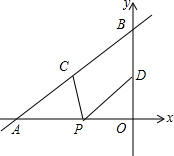 如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )
如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )
 如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )
如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )| A. | 2+$\sqrt{13}$ | B. | 5 | C. | 2$\sqrt{13}$ | D. | 6 |
14.如果二次函数y=x2-6x+8在x的一定取值范围内有最大值(或最小值)为3,满足条件的x的取值范围可以是( )
| A. | -1≤x≤5 | B. | 1≤x≤6 | C. | -2≤x≤4 | D. | -1≤x≤1 |
4.己知在Rt△ABC中,∠C=90°,∠A=α,BC=m,那么AB的长为( )
| A. | $\frac{m}{sinα}$ | B. | mcosα | C. | msinα | D. | $\frac{m}{cosα}$ |
 如图,已知线段AB=a,延长BA至点C,使AC=$\frac{1}{2}$AB.点D为线段BC的中点.
如图,已知线段AB=a,延长BA至点C,使AC=$\frac{1}{2}$AB.点D为线段BC的中点.
