题目内容
14．如果二次函数y=x2-6x+8在x的一定取值范围内有最大值（或最小值）为3，满足条件的x的取值范围可以是（ ）| A． | -1≤x≤5 | B． | 1≤x≤6 | C． | -2≤x≤4 | D． | -1≤x≤1 |
分析 把函数解析式整理成顶点式解析式的形式，然后根据二次函数的最值问题解答．
解答 解：∵y=x2-6x+8=（x-3）2-1，
当y=3时，得出x=1或5，
∴在自变量-1≤x≤1的取值范围内，当x=1时，有最小值3，
故选D．
点评 本题考查了二次函数的最值问题，把函数解析式转化为顶点式形式是解题的关键．
练习册系列答案
一线名师权威作业本系列答案
相关题目
4．下列代数式：$\frac{x}{2}$，$\frac{x}{m}$，2x-y，（1-20%）x，$\sqrt{2}$ab，$\frac{x}{x+y}$，$\root{3}{a}$，其中是整式的个数是（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
2．用不等式表示“a的一半不小于-7”，正确的是（ ）
| A． | $\frac{1}{2}$a≥-7 | B． | $\frac{1}{2}$a≤-7 | C． | $\frac{1}{2}$a＞-7 | D． | $\frac{1}{2}a＜-7$ |
9．在Rt△ABC中，∠C=90°，AC=3，AB=5，则cosA的值为（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{{3\sqrt{34}}}{34}$ |
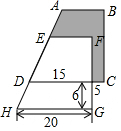如图所示，两个完全相同的直角梯形重叠在一起，将其中一个直角梯形沿AD的方向平移，平移的距离为线段AE的长，求阴影部分的面积．（单位：cm）