题目内容
9.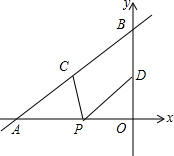 如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )
如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )| A. | 2+$\sqrt{13}$ | B. | 5 | C. | 2$\sqrt{13}$ | D. | 6 |
分析 作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,利用勾股定理即可求出PC+PD的最小值.
解答  解:作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图.
解:作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图.
令y=$\frac{2}{3}$x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y=$\frac{2}{3}$x+4中y=0,则$\frac{2}{3}$x+4=0,解得:x=-6,
∴点A的坐标为(-6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(-3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,-2),
∴PC+PD的最小值=$\sqrt{{3}^{2}+{4}^{2}}$=5,
故选B.
点评 本题考查了一次函数图象上点的坐标特征以及轴对称中最短路径问题,本题属于基础题,难度不大,解决该题型题目时,找出点的坐标利用待定系数法求出D'点的坐标是关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
4.下列代数式:$\frac{x}{2}$,$\frac{x}{m}$,2x-y,(1-20%)x,$\sqrt{2}$ab,$\frac{x}{x+y}$,$\root{3}{a}$,其中是整式的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
18. 如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )
如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )
 如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )
如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )| A. | 12$\sqrt{3}$ | B. | 18 | C. | 6$\sqrt{3}$+6 | D. | 12 |
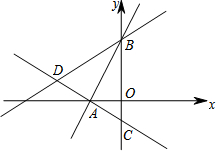 如图,在平面直角坐标系中,过点A的两条直线分别交y轴于B(0,3)、C(0,-1)两点,且∠ABC=30°,AC⊥AB于A.
如图,在平面直角坐标系中,过点A的两条直线分别交y轴于B(0,3)、C(0,-1)两点,且∠ABC=30°,AC⊥AB于A. 如图是一个标准的五角星,将它绕旋转中心旋转x°后能与自身重合,则x的最小值是72°.
如图是一个标准的五角星,将它绕旋转中心旋转x°后能与自身重合,则x的最小值是72°.