题目内容
9.在正方形ABCD中,AB=2,以BC为直径作半圆O.
(1)过点A向半圆O作切线,切点为E(用尺规作图,不写作法,保留作图痕迹).
(2)点P是半圆弧上一动点,当点P运动时,四边形APCE能否成为平行四边形,说明理由.
分析 (1)以点A为圆心,AB长为半径画弧,交半圆于点E,连接AE,则根据SSS即可判定△ABO≌△AEO,进而得到∠ABO=∠AEO=90°,故AE是半圆的切线;
(2)根据AB、AE都是半圆的切线,即可得出AB=AE,再根据AB=BC,可得AE=BC,最后根据当AP∥CE时,CP<BC,即可得到CP<AE,进而得出结论.
解答 解:(1)如图所示,AE即为所求;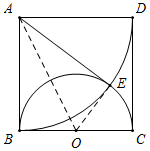
(2)如图所示,四边形APCE不能成为平行四边形.
理由:∵AB、AE都是半圆的切线,
∴AB=AE,
又∵AB=BC,
∴AE=BC,
又∵当AP∥CE时,CP<BC,
∴CP<AE,
∴四边形APCE不能成为平行四边形.
点评 本题主要考查了复杂作图,切线的性质,正方形的性质以及平行四边形的判定,解决问题的关键是掌握:圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目
20.据新华网报道,在新一期全球超级计算机500强榜单中,中国“神威•太湖之光”继续以每秒930 000 000亿次的浮点运算速度领跑,数930 000 000用科学记数法可表示为( )
| A. | 0.93×109 | B. | 9.3×108 | C. | 9.3×109 | D. | 93×107 |
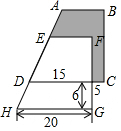 如图所示,两个完全相同的直角梯形重叠在一起,将其中一个直角梯形沿AD的方向平移,平移的距离为线段AE的长,求阴影部分的面积.(单位:cm)
如图所示,两个完全相同的直角梯形重叠在一起,将其中一个直角梯形沿AD的方向平移,平移的距离为线段AE的长,求阴影部分的面积.(单位:cm)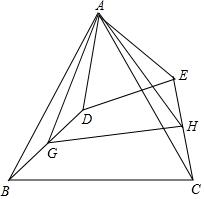 如图,△ABC中,AB=AC,∠BAC=α°(α为已知常数),以A为顶点作△ADE,使∠BAC=∠DAE,AD=AE,G、H分别为BD、CE的中点.
如图,△ABC中,AB=AC,∠BAC=α°(α为已知常数),以A为顶点作△ADE,使∠BAC=∠DAE,AD=AE,G、H分别为BD、CE的中点.