题目内容
12.解不等式组$\left\{\begin{array}{l}{-3(x-2)≥4-x}\\{\frac{1+4x}{3}>x}\end{array}\right.$并在数轴上表示出它的解集.分析 先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.
解答 解:$\left\{\begin{array}{l}{-3(x-2)≥4-x①}\\{\frac{1+4x}{3}>x②}\end{array}\right.$
由①得:x≤1,
由②得:x>-1.
在数轴上表示为: ,
,
则不等式组的解集是:-1<x≤1.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
相关题目
20.小华通过学习函数发现:若二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,y1),(x2,y2)(x1<x2),若y1y2<0,则方程ax2+bx+c=0(a≠0)的一个根x0的取值范围是x1<x0<x2,请你类比此方法,推断方程x3+x-1=0的实数根x0所在范围为( )
| A. | -$\frac{1}{2}$<x0<0 | B. | 0<x0<$\frac{1}{2}$ | C. | $\frac{1}{2}$<x0<1 | D. | 1<x0<$\frac{3}{2}$ |
17.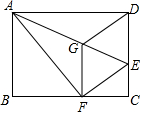 如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
①∠ADG=∠AFG;②四边形DEFG是菱形;③DG2=$\frac{1}{2}$AE•EG;④若AB=4,AD=5,则CE=1.
 如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )①∠ADG=∠AFG;②四边形DEFG是菱形;③DG2=$\frac{1}{2}$AE•EG;④若AB=4,AD=5,则CE=1.
| A. | ①②③④ | B. | ①②③ | C. | ①③④ | D. | ①② |
1.已知关于x的一元二次方程mx2+2x-1=0有两实数根,则m的取值范围是( )
| A. | m>1 | B. | m≥-1 | C. | m>-1且m≠0 | D. | m≥-1且m≠0 |
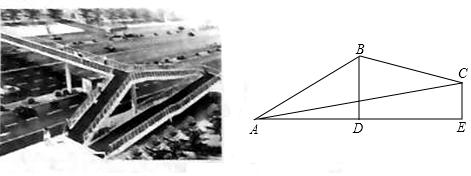
 如图,直线AB与⊙O相交于C、D两点,CE是⊙O的直径,CF平分∠BCE交⊙O于点F,过点F作FG⊥AB,垂足为点G,连接DF.
如图,直线AB与⊙O相交于C、D两点,CE是⊙O的直径,CF平分∠BCE交⊙O于点F,过点F作FG⊥AB,垂足为点G,连接DF.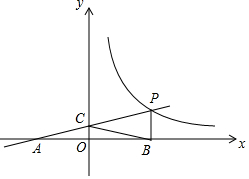 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.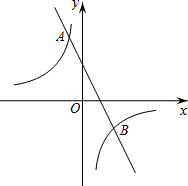 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).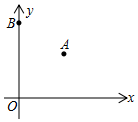 平面直角坐标系中,A(3,3)、B(0,5).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
平面直角坐标系中,A(3,3)、B(0,5).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )