题目内容
如图1,矩形ABCD的边AD在y轴上,抛物线y=x2-4x+3经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上.
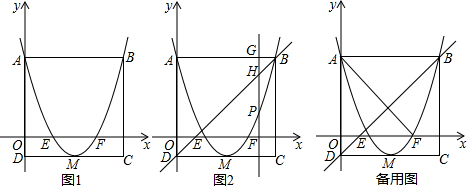
(1)请直接写出下列各点的坐标:A ,B ,C ,D ;
(2)若点P是抛物线上一动点(点P不与点A、点B重合),过点P作y轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2.
①当线段PH=2GH时,求点P的坐标;
②当点P在直线BD下方时,点K在直线BD上,且满足△KPH∽△AEF,求△KPH面积的最大值.

(1)请直接写出下列各点的坐标:A
(2)若点P是抛物线上一动点(点P不与点A、点B重合),过点P作y轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2.
①当线段PH=2GH时,求点P的坐标;
②当点P在直线BD下方时,点K在直线BD上,且满足△KPH∽△AEF,求△KPH面积的最大值.
考点:二次函数综合题,矩形的性质,相似三角形的性质
专题:压轴题
分析:(1)令x=0,得到点A的坐标,再根据点A的纵坐标得到点B的坐标,根据抛物线的顶点式和矩形的性质可得C.D的坐标;
(2)①根据待定系数法可得直线BD的解析式,设点P的坐标为(x,x2-4x+3),则点H(x,x-1),点G(x,3).分三种情况:1°当x≥1且x≠4时;2°当0<x<1时;3°当x<0时;三种情况讨论可得点P的坐标;
②根据相似三角形的性质可得s△KPH=
PH2=
(-x2+5x-4)2,再根据二次函数的增减性可得△KPH面积的最大值.
(2)①根据待定系数法可得直线BD的解析式,设点P的坐标为(x,x2-4x+3),则点H(x,x-1),点G(x,3).分三种情况:1°当x≥1且x≠4时;2°当0<x<1时;3°当x<0时;三种情况讨论可得点P的坐标;
②根据相似三角形的性质可得s△KPH=
| 3 |
| 4 |
| 3 |
| 4 |
解答:解:(1)A(0,3),B(4,3),C(4,-1),D(0,-1).
(2)①设直线BD的解析式为y=kx+b(k≠0),由于直线BD经过D(0,-1),B(4,3),
∴
,
解得
,
∴直线BD的解析式为y=x-1.
设点P的坐标为(x,x2-4x+3),则点H(x,x-1),点G(x,3).
1°当x≥1且x≠4时,点G在PH的延长线上,如图①.
∵PH=2GH,
∴(x-1)-(x2-4x+3)=2[3-(x-1)],
∴x2-7x+12=0,
解得x1=3,x2=4.
当x2=4时,点P,H,G重合于点B,舍去.
∴x=3.
∴此时点P的坐标为(3,0).

2°当0<x<1时,点G在PH的反向延长线上,如图②,PH=2GH不成立.
3°当x<0时,点G在线段PH上,如图③.
∵PH=2GH,
∴(x2-4x+3)-(x-1)=2[3-(x-1)],
∴x2-3x-4=0,解得x1=-1,x2=4(舍去),
∴x=-1.此时点P的坐标为(-1,8).
综上所述可知,点P的坐标为(3,0)或(-1,8).
②如图④,令x2-4x+3=0,得x1=1,x2=3,

∴E(1,0),F(3,0),
∴EF=2.
∴S△AEF=
EF•OA=3.
∵△KPH∽△AEF,
∴
=(
)2,
∴s△KPH=
PH2=
(-x2+5x-4)2.
∵1<x<4,
∴当x=
时,s△KPH的最大值为
.
(2)①设直线BD的解析式为y=kx+b(k≠0),由于直线BD经过D(0,-1),B(4,3),
∴
|
解得
|
∴直线BD的解析式为y=x-1.
设点P的坐标为(x,x2-4x+3),则点H(x,x-1),点G(x,3).
1°当x≥1且x≠4时,点G在PH的延长线上,如图①.
∵PH=2GH,
∴(x-1)-(x2-4x+3)=2[3-(x-1)],
∴x2-7x+12=0,
解得x1=3,x2=4.
当x2=4时,点P,H,G重合于点B,舍去.
∴x=3.
∴此时点P的坐标为(3,0).

2°当0<x<1时,点G在PH的反向延长线上,如图②,PH=2GH不成立.
3°当x<0时,点G在线段PH上,如图③.
∵PH=2GH,
∴(x2-4x+3)-(x-1)=2[3-(x-1)],
∴x2-3x-4=0,解得x1=-1,x2=4(舍去),
∴x=-1.此时点P的坐标为(-1,8).
综上所述可知,点P的坐标为(3,0)或(-1,8).
②如图④,令x2-4x+3=0,得x1=1,x2=3,

∴E(1,0),F(3,0),
∴EF=2.
∴S△AEF=
| 1 |
| 2 |
∵△KPH∽△AEF,
∴
| s△KPH |
| s△AEF |
| PH |
| EF |
∴s△KPH=
| 3 |
| 4 |
| 3 |
| 4 |
∵1<x<4,
∴当x=
| 5 |
| 2 |
| 243 |
| 64 |
点评:考查了二次函数综合题,涉及的知识点有:坐标轴上的点的坐标特征,抛物线的顶点式,矩形的性质,待定系数法求直线的解析式,相似三角形的性质,二次函数的增减性,分类思想,综合性较强,有一定的难度..

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
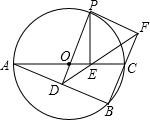 如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.
如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.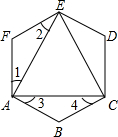 如图,已知六边形ABCDEF的内角都相等,且∠1=∠2,∠3=∠4.求∠CAE的度数.
如图,已知六边形ABCDEF的内角都相等,且∠1=∠2,∠3=∠4.求∠CAE的度数.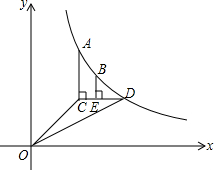 如图,已知函数y=
如图,已知函数y= 如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为
如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为 如图,在五边形ABCDE中,若∠D=95°,则∠1+∠2+∠3+∠4=
如图,在五边形ABCDE中,若∠D=95°,则∠1+∠2+∠3+∠4=