题目内容
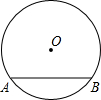 如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为
如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为考点:垂径定理,勾股定理
专题:
分析:作OC⊥AB于C,连接OA,根据垂径定理得到AC=BC=
AB=3,然后在Rt△AOC中利用勾股定理计算OC即可.
| 1 |
| 2 |
解答: 解:作OC⊥AB于C,连结OA,如图,
解:作OC⊥AB于C,连结OA,如图,
∵OC⊥AB,
∴AC=BC=
AB=
×8=4,
在Rt△AOC中,OA=5,
∴OC=
=
=3,
即圆心O到AB的距离为3.
故答案为:3.
 解:作OC⊥AB于C,连结OA,如图,
解:作OC⊥AB于C,连结OA,如图,∵OC⊥AB,
∴AC=BC=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOC中,OA=5,
∴OC=
| OA2-AC2 |
| 52-42 |
即圆心O到AB的距离为3.
故答案为:3.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
下列四个实数中,是无理数的为( )
| A、0 | ||
| B、-3 | ||
C、
| ||
D、
|
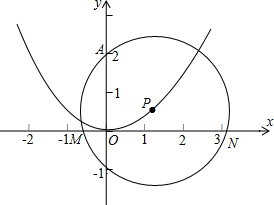 如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(
如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(
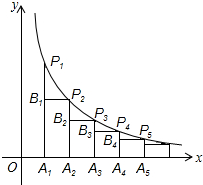 如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点做x轴的垂线与反比例函数y=
如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点做x轴的垂线与反比例函数y= 如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为
如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为