题目内容
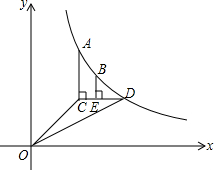 如图,已知函数y=
如图,已知函数y=| k |
| x |
(1)求△OCD的面积;
(2)当BE=
| 1 |
| 2 |
考点:反比例函数系数k的几何意义,反比例函数图象上点的坐标特征
专题:代数几何综合题
分析:(1)根据待定系数法,可得函数解析式,根据图象上的点满足函数解析式,可得D点坐标,根据三角形的面积公式,可得答案;
(2)根据BE的长,可得B点的纵坐标,根据点在函数图象上,可得B点横坐标,根据两点间的距离公式,可得答案.
(2)根据BE的长,可得B点的纵坐标,根据点在函数图象上,可得B点横坐标,根据两点间的距离公式,可得答案.
解答:解;(1)y=
(x>0)的图象经过点A(1,2),
∴k=2.
∵AC∥y轴,AC=1,
∴点C的坐标为(1,1).
∵CD∥x轴,点D在函数图象上,
∴点D的坐标为(2,1).
∴S△OCD=
×1×1=
.
(2)∵BE=
AC,
∴BE=
.
∵BE⊥CD,
点B的纵坐标=2-
=
,
由反比例函数y=
,
点B的横坐标x=2÷
=
,
∴点B的横坐标是
,纵坐标是
.
∴CE=
-1=
.
| k |
| x |
∴k=2.
∵AC∥y轴,AC=1,
∴点C的坐标为(1,1).
∵CD∥x轴,点D在函数图象上,
∴点D的坐标为(2,1).
∴S△OCD=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵BE=
| 1 |
| 2 |
∴BE=
| 1 |
| 2 |
∵BE⊥CD,
点B的纵坐标=2-
| 1 |
| 2 |
| 3 |
| 2 |
由反比例函数y=
| 2 |
| x |
点B的横坐标x=2÷
| 3 |
| 2 |
| 4 |
| 3 |
∴点B的横坐标是
| 4 |
| 3 |
| 3 |
| 2 |
∴CE=
| 4 |
| 3 |
| 1 |
| 3 |
点评:本题考查了反比例函数k的几何意义,利用待定系数法求解析式,图象上的点满足函数解析式.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
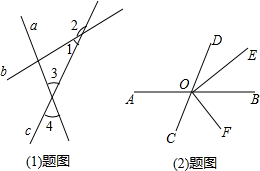 (1)如图,直线a,b,c两两相交,∠3=2∠1,∠2=155°,求∠4的度数.
(1)如图,直线a,b,c两两相交,∠3=2∠1,∠2=155°,求∠4的度数.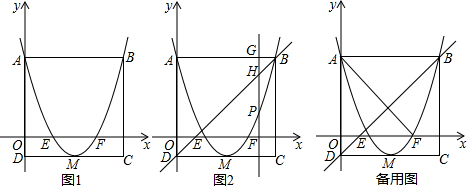
 如图,AF平分∠BAC,DF平分∠BDC,求证:∠AFD=
如图,AF平分∠BAC,DF平分∠BDC,求证:∠AFD=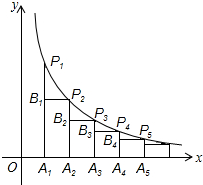 如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点做x轴的垂线与反比例函数y=
如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点做x轴的垂线与反比例函数y= 如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为
如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为