题目内容
12.同学们都知道,|5-(-2)|表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对的两点之间的距离.试探索(1)求|5-(-2)|=7;
(2)同样道理|x+1008|=|x-1005|表示数轴上有理数x所对点到-1008和1005所对的两点距离相等,则x=-1.5
(3)类似的|x+5|+|x-2|表示数轴上有理数x所对点到-5和2所对的两点距离之和,请你找出所有符合条件的整数x,使得|x+5|+|x-2|=7,这样的整数是-5,-4,-3,-2,-1,0,1,2.
(4)由以上探索猜想对于任何有理数x,|x-3|+|x-6|是否有最小值?如果有,写出最小值;如果没有,说明理由.
分析 (1)5与-2两数在数轴上所对的两点之间的距离为5-(-2)=7;
(2)在数轴上,找到-1008和1005的中点坐标即可求解;
(3)利用数轴解决:把|x+5|+|x-2|=6理解为:在数轴上,某点到-5所对应的点的距离和到2所对应的点的距离之和为7,然后根据数轴可写出满足条件的整数x;
(4)把丨x-3丨+丨x-6丨理解为:在数轴上表示x到3和6的距离之和,求出表示3和6的两点之间的距离即可.
解答 解:(1)|5-(-2)|=7;
(2)(-1008+1005)÷2=-1.5;
(3)式子|x+5|+|x-2|=6理解为:在数轴上,某点到-5所对应的点的距离和到2所对应的点的距离之和为7,
所以满足条件的整数x可为-5,-4,-3,-2,-1,0,1,2;
(4)有,最小值为-3-(-6)=3.
故答案为:7;-1.5;-5,-4,-3,-2,-1,0,1,2.
点评 此题主要考查了去绝对值和数轴相联系的综合试题以及去绝对值的方法和去绝对值在数轴上的运用,难度较大,去绝对的关键是确定绝对值里面的数的正负性.

练习册系列答案
相关题目
2.二次函数y=$\frac{1}{2}$(x-2)2-1图象的顶点坐标是( )
| A. | (-2,-1) | B. | (2,-1) | C. | (-2,1) | D. | (2,1) |
 如图所示,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
如图所示,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.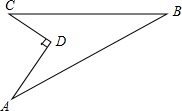 如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米300元,试问用该草坪铺满这块空地共需花费多少元?
如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米300元,试问用该草坪铺满这块空地共需花费多少元?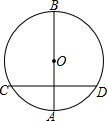 如图,AB是⊙O的直径,弦CD垂直平分OA,求劣弧CD所对的圆周角的度数.
如图,AB是⊙O的直径,弦CD垂直平分OA,求劣弧CD所对的圆周角的度数.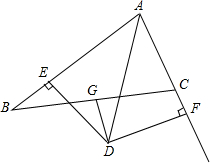 如图,△ABC中,∠A的平分线与BC的中垂线交于D点,过D作DE⊥AB于E,DF⊥AC于F,判断BE与CF的数量关系,并说明理由.
如图,△ABC中,∠A的平分线与BC的中垂线交于D点,过D作DE⊥AB于E,DF⊥AC于F,判断BE与CF的数量关系,并说明理由.