题目内容
7.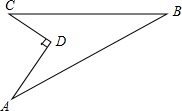 如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米300元,试问用该草坪铺满这块空地共需花费多少元?
如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米300元,试问用该草坪铺满这块空地共需花费多少元?
分析 连接AC,根据勾股定理求出AC,根据勾股定理的逆定理求出∠ACB=90°,求出区域的面积,即可求出答案.
解答 解:连结AC, 如图所示:
如图所示:
在Rt△ACD中,∠ADC=90°,AD=4米,CD=3米,
由勾股定理得:AC=$\sqrt{{8}^{2}+{6}^{2}}$=10(米),
∵AC2+BC2=102+242=676,AB2=262=676,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴该区域面积S=S△ACB-S△ADC=$\frac{1}{2}$×10×24-$\frac{1}{2}$×6×8=96(平方米),
∴铺满这块空地共需花费=96×300=28800元.
点评 本题考查了勾股定理的应用,三角形面积,勾股定理的逆定理等知识,解此题的关键是求出区域的面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 小强有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各题:
小强有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各题: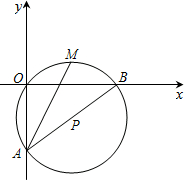 如图在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上,M为劣弧OB的中点.
如图在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上,M为劣弧OB的中点.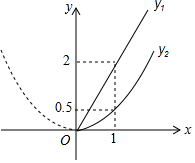 随着成都市近几年城市建设的快速发展,对花木的需求量逐年提高,某园林专业户计划投资种植树木及花卉,根据市场调查与预测,种植树木的利润y1与投入资金x成正比例函数关系;种植花卉的利润y2与投入资金x成二次函数关系,如图所示(利润与投入资金的单位:万元)
随着成都市近几年城市建设的快速发展,对花木的需求量逐年提高,某园林专业户计划投资种植树木及花卉,根据市场调查与预测,种植树木的利润y1与投入资金x成正比例函数关系;种植花卉的利润y2与投入资金x成二次函数关系,如图所示(利润与投入资金的单位:万元) 如图,已知△ABC中,AB=AC=5,BC=6.
如图,已知△ABC中,AB=AC=5,BC=6.