题目内容
17．
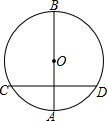如图，AB是⊙O的直径，弦CD垂直平分OA，求劣弧CD所对的圆周角的度数．
分析 设⊙O半径为R，连接OC，OD，求出OC=R，OM=$\frac{1}{2}$R，∠CMO=90°，根据含30度角的直角三角形性质求出∠OCM=30°，推出∠COM=60°即可．
解答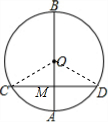 
解：设⊙O半径为R，连接OC，OD，
∵⊙O的直径为AB，弦CD垂直平分OA，
∴OC=R，OM=$\frac{1}{2}$R，∠CMO=90°，
∴∠OCM=30°，
∴∠COM=60°
同理∠DOM=60°，
∴∠COD=120°，
∴劣弧CD所对的圆周角的度数=$\frac{1}{2}$∠COD=60°．
点评 本题考查了含30度角的直角三角形性质，三角形内角和定理，圆心角、弧、弦之间的关系等知识点的应用，关键是求出角COM的度数．
练习册系列答案
相关题目
如图所示，△ABC中，∠B=30°，∠C=45°，AC=2，求AB和BC的长．
如图，点A、P、B、C是⊙O上的四点，且满足∠BAC=∠APC=60°，求证：△ABC是等边三角形．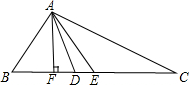
如图，在△ABC中，AE是中线，AD是角平分线，AF是高，则：
如图，BC是⊙O的一个内接正五边形的一边，请用等分圆周的方法，在⊙A中用尺规作图作出一个⊙A的内接正五边形（请保留作图痕迹）．