题目内容
1.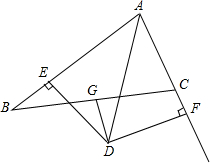 如图,△ABC中,∠A的平分线与BC的中垂线交于D点,过D作DE⊥AB于E,DF⊥AC于F,判断BE与CF的数量关系,并说明理由.
如图,△ABC中,∠A的平分线与BC的中垂线交于D点,过D作DE⊥AB于E,DF⊥AC于F,判断BE与CF的数量关系,并说明理由.
分析 连接DB、DC,根据线段垂直平分线的性质和角平分线的性质得到DB=DC,DE=DF,证明Rt△BDE≌Rt△CDF,根据全等三角形的性质证明结论.
解答 解:BE=CF,
理由如下:连接DB,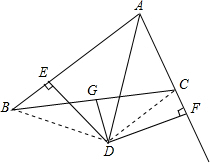 CD,
CD,
∵DG是BC的垂直平分线,
∴DB=DC,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△BDE和Rt△CDF中,
$\left\{\begin{array}{l}{DB=DC}\\{DE=DF}\end{array}\right.$,
∴Rt△BDE≌Rt△CDF,
∴BE=CF.
点评 本题考查的是线段垂直平分线的性质,线段的垂直平分线上的点到线段的两个端点的距离相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.计算2120+(-2)120所得的正确结果是( )
| A. | 2120 | B. | -2120 | C. | 2121 | D. | 2 |
 如图,已知△ABC中,AB=AC=5,BC=6.
如图,已知△ABC中,AB=AC=5,BC=6. 如图,BC是⊙O的一个内接正五边形的一边,请用等分圆周的方法,在⊙A中用尺规作图作出一个⊙A的内接正五边形(请保留作图痕迹).
如图,BC是⊙O的一个内接正五边形的一边,请用等分圆周的方法,在⊙A中用尺规作图作出一个⊙A的内接正五边形(请保留作图痕迹).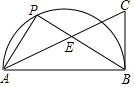 如图,P是AB为直径的半圆周上一点,点C在∠PAB的平分线上,且CB⊥AB于B,PB交AC于E,若AB=4,BE=2,则PE的长为$\frac{6}{5}$.
如图,P是AB为直径的半圆周上一点,点C在∠PAB的平分线上,且CB⊥AB于B,PB交AC于E,若AB=4,BE=2,则PE的长为$\frac{6}{5}$.