题目内容
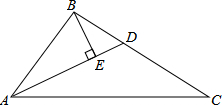 如图,在△ABC中,∠BAC=60°,AD是△ABC的角平分线,BE⊥AD于点E,AB=6,AC=10,则DE=
如图,在△ABC中,∠BAC=60°,AD是△ABC的角平分线,BE⊥AD于点E,AB=6,AC=10,则DE=考点:相似三角形的判定与性质,等边三角形的判定与性质,三角形中位线定理
专题:
分析:如图,作辅助线;求出线段BE、CF、BG的长度;运用S△ABC=S△ABD+S△ACD,求出AD的长度,即可解决问题.
解答: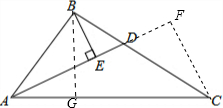 解:如图,过点B作BG⊥AC于点G;
解:如图,过点B作BG⊥AC于点G;
过点C作CF⊥AD,交AD的延长线于点F;
∵∠BAC=60°,AD平分∠BAC,BE⊥AE,
∴∠BAE=30°,BE=
AB=3,AE=3
,BG=AB•sin60°=3
;
由角平分线的性质得:
=
=
①;
∵BE⊥EF,CF⊥EF,
∴BE∥CF,△BDE∽△CDF,
∴
=
②,联立①②并求得:CF=5;
∵S△ABC=S△ABD+S△ACD,
∴
AC•BG=
AD•BE+
AD•CF,
∴AD=
,DE=AD-AE=
-3
=
,
故答案为:
.
 解:如图,过点B作BG⊥AC于点G;
解:如图,过点B作BG⊥AC于点G;过点C作CF⊥AD,交AD的延长线于点F;
∵∠BAC=60°,AD平分∠BAC,BE⊥AE,
∴∠BAE=30°,BE=
| 1 |
| 2 |
| 3 |
| 3 |
由角平分线的性质得:
| BD |
| CD |
| AB |
| AC |
| 6 |
| 10 |
∵BE⊥EF,CF⊥EF,
∴BE∥CF,△BDE∽△CDF,
∴
| BE |
| CF |
| BD |
| CD |
∵S△ABC=S△ABD+S△ACD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
15
| ||
| 4 |
15
| ||
| 4 |
| 3 |
3
| ||
| 4 |
故答案为:
3
| ||
| 4 |
点评:该题主要考查了相似三角形的判定及其性质、直角三角形的边角关系等几何知识点及其应用问题;解题的关键是作辅助线,构造相似三角形,借助三角形的面积公式来分析、解答.

练习册系列答案
相关题目
已知点(-1,y1),(2,y2),(3,y3)在二次函数y=x2-4x-5的图象上,则下列结论正确的是( )
| A、y1>y2>y3 |
| B、y1>y3>y2 |
| C、y3>y1>y2 |
| D、y2>y3>y1 |
 在△ABC中,∠B=63°,∠C=46°,AD和AE分别是它的高和角平分线,求∠DAE的度数.
在△ABC中,∠B=63°,∠C=46°,AD和AE分别是它的高和角平分线,求∠DAE的度数.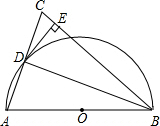 如图,在△ABC中,BA=BC,以AB为直径作半圆⊙O,交AC于点D.连结DB,过点D 作DE⊥BC,垂足为点E.
如图,在△ABC中,BA=BC,以AB为直径作半圆⊙O,交AC于点D.连结DB,过点D 作DE⊥BC,垂足为点E.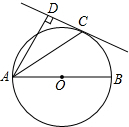 如图所示,AB是⊙O的直径,点C在⊙O上,AC平分∠DAB,AD⊥CD.求证:CD与⊙O相切.
如图所示,AB是⊙O的直径,点C在⊙O上,AC平分∠DAB,AD⊥CD.求证:CD与⊙O相切.