题目内容
已知OA⊥OC，∠AOB与∠AOC的度数之比为3：5，则∠BOC等于 ．
考点：垂线
专题：
分析：根据垂直定义知∠AOC=90°，由∠AOB：∠AOC=3：5，可求∠AOB，根据∠AOB与∠AOC的位置关系，分类求解．
解答：
解：∵OA⊥OC，
∴∠AOC=90°，
∵∠AOB：∠AOC=3：5，
∴∠AOB=54°．
因为∠AOB的位置有两种：一种是在∠AOC内，一种是在∠AOC外．
①当在∠AOC内时，∠BOC=90°-54°=36°；
②当在∠AOC外时，∠BOC=90°+54°=144°．
故答案是：36°或144°．
解：∵OA⊥OC，∴∠AOC=90°，
∵∠AOB：∠AOC=3：5，
∴∠AOB=54°．
因为∠AOB的位置有两种：一种是在∠AOC内，一种是在∠AOC外．
①当在∠AOC内时，∠BOC=90°-54°=36°；
②当在∠AOC外时，∠BOC=90°+54°=144°．
故答案是：36°或144°．
点评：此题主要考查了垂直的定义：当两条直线相交所成的四个角中，有一个角是直角时，即两条直线互相垂直．分类讨论是解题的关键．
练习册系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
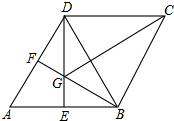如图，在菱形ABCD中，∠A=60°，E、F分别是AB、AD的中点，DE、BF相交于点G，连接BD、CG．给出以下结论，其中正确的有（ ）①∠BGD=120°；②BG+DG=CG；③△BDF≌△CGB；④S△ADE=
| ||
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列式子中：①3x-5；②2a-3=0；③7＞-3；④5-7=-2；⑤|x|=1；⑥2x2+x=1．是等式的有（ ）
| A、6个 | B、5个 | C、4个 | D、3个 |
下列说法不正确的是（ ）
| A、O是正整数 |
| B、O是非负数 |
| C、没有最大的正数 |
| D、有理数分为整数和分数 |
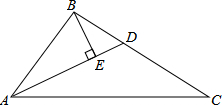如图，在△ABC中，∠BAC=60°，AD是△ABC的角平分线，BE⊥AD于点E，AB=6，AC=10，则DE=