题目内容
如图，有一长方体，已知侧面ABCD为正方形，边长为5，BB′=7，现有一绳子从A出发，沿正方体表面到达C′处，问绳子最短是多少米？考点：平面展开-最短路径问题
专题：
分析：把长方体展开，然后利用勾股定理列式求解即可．
解答：解：如图，AB′=5+7=12，
由勾股定理得，AC′=
=
=13，
故绳子最短是13米．
由勾股定理得，AC′=
| AB′2+B′C′2 |
| 122+52 |
故绳子最短是13米．
点评：本题考查了长方体侧面展开图确定最短路径问题，理解展开图中路径所在的直角三角形是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
二次函数y=（x-2）2+k的图象的顶点在反比例函数y=
的图象上，则k=（ ）
| 1 |
| x |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
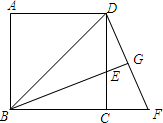已知，如图，BD是正方形ABCD的对角线，BE平分∠DBC，交DC于点E，延长BC到点F，使CF=CE，连接DF，交BE的延长线于点G，求证：
如图，已知△ABC中，AB的垂直平分线交BC于D，AC的垂直平分线交BC于E，M，N为垂足，若BD=3，DE=4，EC=5，求证：∠B=45°．