Question

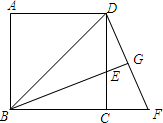已知，如图，BD是正方形ABCD的对角线，BE平分∠DBC，交DC于点E，延长BC到点F，使CF=CE，连接DF，交BE的延长线于点G，求证：
（1）△BCE≌△DCF；
（2）DG²=GE•GB；
（3）若CF=2

2

-2，求正方形ABCD的面积．

Answer 1

考点：相似三角形的判定与性质,全等三角形的判定与性质,正方形的性质

专题：

分析：（1）根据正方形的性质得正方形，CB=CD，∠BCD=90°，利用“SAS”可判断△BCE≌△DCF；
（2）由△BCE≌△DCF得∠CBE=∠CDF，再根据角平分线的定义得到∠CBE=∠DBE，则∠DDG=∠GBD，而∠DGE=∠BGD，根据三角形相似的判定得到△GDE∽△GBD，利用相似比即可得到DG²=GE•GB；
（3）先利用等角的余角相等得∠DGE=∠BCE=90°，即BG⊥DF，而BG平分∠DBF，根据等腰三角形的判定方法得到△BGF为等腰三角形，则BD=BF=BC+CF，由于BD=

2

BC，CF=2

2

-2，所以

2

BC=BC+2

2

-2，可计算出BC=2，然后计算正方形ABCD的面积．

解答：证明：（1）∵四边形ABCD为正方形，
∴CB=CD，∠BCD=90°，
在△BCE和△DCF中

BC=DC ∠BCE=∠DCF CE=CF

，
∴△BCE≌△DCF（SAS）；
（2）∵△BCE≌△DCF，
∴∠CBE=∠CDF，
∵BE平分∠DBC，
∴∠CBE=∠DBE，
∴∠DDG=∠GBD，
而∠DGE=∠BGD，
∴△GDE∽△GBD，
∴DG：GE=GB：DG，
∴DG²=GE•GB；
（3）∵∠CBE=∠CDF，
而∠CEB=∠GED，
∴∠DGE=∠BCE=90°，
∴BG⊥DF，
而BG平分∠DBF，
∴△BGF为等腰三角形，
∴BD=BF=BC+CF，
∵BD=

2

BC，CF=2

2

-2，
∴

2

BC=BC+2

2

-2，
∴BC=2，
∴正方形ABCD的面积为4．

点评：本题考查了相似三角形的判定与性质：有两组角对应相等的两个三角形相似；相似三角形的对应角相等，对应边的比相等．也考查了三角形全等的判定与性质、正方形的性质．