题目内容
11. 如图,△ABC中,AB=AC,O是BC的中点,⊙O与AB相切于点D,求证:AC是⊙O的切线.
如图,△ABC中,AB=AC,O是BC的中点,⊙O与AB相切于点D,求证:AC是⊙O的切线.
分析 过点O作OE⊥AC于点E,连结OD,OA,根据切线的性质得出AB⊥OD,根据等腰三角形三线合一的性质得出AO是∠BAC的平分线,根据角平分线的性质得出OE=OD,从而证得结论.
解答 证明:过点O作OE⊥AC于点E,连结OD,OA,
∵AB与⊙O相切于点D,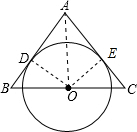
∴AB⊥OD,
∵△ABC为等腰三角形,O是底边BC的中点,
∴AO是∠BAC的平分线,
∴OE=OD,即OE是⊙O的半径,
∵AC经过⊙O的半径OE的外端点且垂直于OE,
∴AC是⊙O的切线.
点评 本题考查了切线的判定和性质,等腰三角形的性质,角平分线的性质,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
3.某种计算机完成一次基本运算的时间约为0.000000005s,把0.000000005s用科学记数法可以表示为( )
| A. | 0.5×10-8s | B. | 5×10-9s | C. | 5×10-8s | D. | 0.5×10-9s |
20.下列各式计算正确的是( )
| A. | a2+2a3=3a5 | B. | a•a2=a3 | C. | a6÷a2=a3 | D. | (a2)3=a5 |
1.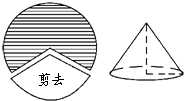 如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )
如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )
 如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )
如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )| A. | 12cm | B. | 8cm | C. | 20cm | D. | 18cm |
 如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.求证:AC平分∠DAB.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.求证:AC平分∠DAB. 某商场新进一种商品,进货价为30元/件,按物价局规定,商品售价在30~70元之间,(包括30元和70元),经过一段销售发现,商品销量y(件/天)与售价x(元/件)之间满足一次函数关系,如图所示.
某商场新进一种商品,进货价为30元/件,按物价局规定,商品售价在30~70元之间,(包括30元和70元),经过一段销售发现,商品销量y(件/天)与售价x(元/件)之间满足一次函数关系,如图所示.