题目内容
2．
如图，AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D．求证：AC平分∠DAB．
分析 连结OC，如图，根据切线的性质得OC⊥AD，则可得到OC∥AD，根据平行线的性质得∠1=∠2，加上∠1=∠3，则∠2=∠3，于是可判断AC平分∠DAB．
解答 
证明：连结OC，如图，
∵CD为⊙O的切线，
∴OC⊥AD，
∵AD⊥CD，
∴OC∥AD，
∴∠1=∠2，
∵OC=OA，
∴∠1=∠3，
∴∠2=∠3，
∴AC平分∠DAB．
点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了圆周角定理．
练习册系列答案
相关题目
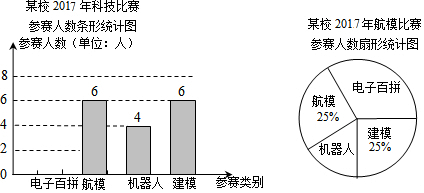
10．王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图：
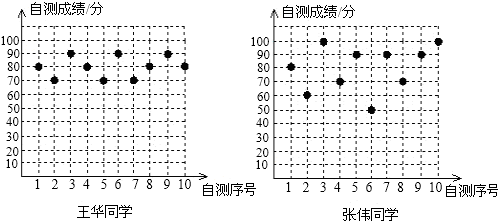
（1）根据图中提供的数据列出如下统计表：
则a=80，b=80，c=90，d=60，
（2）将90分以上（含90分）的成绩视为优秀，则优秀率高的是张伟．
（3）现在要从这两个同学选一位去参加数学竞赛，你可以根据以上的数据给老师哪些建议？
（1）根据图中提供的数据列出如下统计表：
| 平均成绩（分） | 中位数（分） | 众数（分） | 方差（S2） | |
| 王华 | 80 | b | 80 | d |
| 张伟 | a | 85 | c | 260 |
（2）将90分以上（含90分）的成绩视为优秀，则优秀率高的是张伟．
（3）现在要从这两个同学选一位去参加数学竞赛，你可以根据以上的数据给老师哪些建议？
如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点P从点A出发沿边AC向点C以每秒1个单位长度的速度运动，同时点Q从点C出发沿边CB向点B以每秒a个单位长度的速度运动，过点P作PD⊥BC，交AB于点D，连接PQ．当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒（t≥0）．
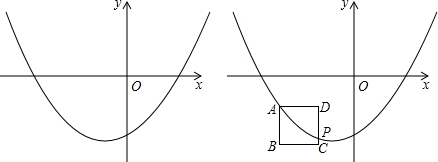
如图，△ABC中，AB=AC，O是BC的中点，⊙O与AB相切于点D，求证：AC是⊙O的切线．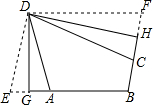
定义：有三个内角相等凸四边形叫三等角四边形．