题目内容
1.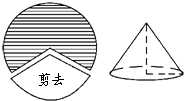 如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )
如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )| A. | 12cm | B. | 8cm | C. | 20cm | D. | 18cm |
分析 设圆锥的底面圆半径为r,先利用圆的周长公式计算出剩下的扇形的弧长,然后把它作为圆锥的底面圆的周长进行计算即可.
解答 解:设圆锥的底面圆半径为r,
∵半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,
∴剩下的扇形的弧长=$\frac{3}{5}$•2π•15=18π,
∴2π•r=18π,
∴r=9,
∴圆锥的高为$\sqrt{1{5}^{2}-{9}^{2}}$=12cm.
故选A.
点评 本题考查了圆锥的有关计算:圆锥的侧面展开图为扇形,圆锥的底面圆的周长等于扇形的弧长.也考查了圆的周长公式.

练习册系列答案
相关题目
9.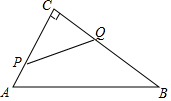 如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
 如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )| A. | 19cm2 | B. | 16cm2 | C. | 15cm2 | D. | 12cm2 |
16.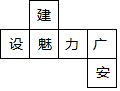 如图是一个正方体的表面展开图,则原正方体中与“魅”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“魅”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“魅”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“魅”字所在的面相对的面上标的字是( )| A. | 建 | B. | 力 | C. | 广 | D. | 安 |
6.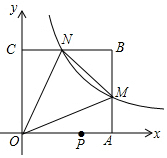 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )| A. | 6$\sqrt{2}$ | B. | 10 | C. | 2$\sqrt{26}$ | D. | 2$\sqrt{29}$ |
10.下列国旗图案是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,△ABC中,AB=AC,O是BC的中点,⊙O与AB相切于点D,求证:AC是⊙O的切线.
如图,△ABC中,AB=AC,O是BC的中点,⊙O与AB相切于点D,求证:AC是⊙O的切线.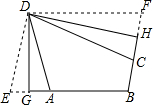 定义:有三个内角相等凸四边形叫三等角四边形.
定义:有三个内角相等凸四边形叫三等角四边形.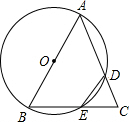 如图,已知等边△ABC的边长为6,以AB为直径的⊙O与边AC、BC分别交于D、E两点,则劣弧$\widehat{DE}$的长为π.
如图,已知等边△ABC的边长为6,以AB为直径的⊙O与边AC、BC分别交于D、E两点,则劣弧$\widehat{DE}$的长为π.