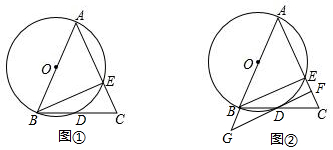题目内容
6.如图,一次函数y=ax+b(a≠0)与二次函数y=ax2+bx(a≠0)图象大致是( )| A. | 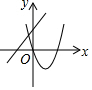 | B. | 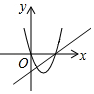 | C. | 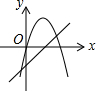 | D. | 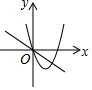 |
分析 利用一次函数的图象的性质确定a、b的符号,然后看二次函数是否符合即可确定正确的选项.
解答 解:A、一次函数y=ax+b(a≠0)中a>0,b>0,二次函数y=ax2+bx(a≠0)中a>0,b<0,故错误,不符合题意;
B、一次函数y=ax+b(a≠0)中a>0,b<0,二次函数y=ax2+bx(a≠0)中a>0,b<0,故正确,符合题意;
C、一次函数y=ax+b(a≠0)中a>0,b<0,二次函数y=ax2+bx(a≠0)中a<0,b>0,故错误,不符合题意;
D、一次函数y=ax+b(a≠0)中a>0,b=0,二次函数y=ax2+bx(a≠0)中a>0,b<0,故错误,不符合题意;
故选B.
点评 考查了二次函数的图象与一次函数的图象的知识,解题的关键是了解各个函数的图象与系数的关系,难度不大.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
1. 如图,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2017C2017,则m的值和点C2017的坐标是( )
如图,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2017C2017,则m的值和点C2017的坐标是( )
 如图,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2017C2017,则m的值和点C2017的坐标是( )
如图,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2017C2017,则m的值和点C2017的坐标是( )| A. | 2,(-22017,22017×$\sqrt{3}$) | B. | 2,(-22018,0) | ||
| C. | $\sqrt{3}$,(-22017,22017×$\sqrt{3}$) | D. | $\sqrt{3}$,(-22018,0) |
15.下列图案是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.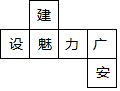 如图是一个正方体的表面展开图,则原正方体中与“魅”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“魅”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“魅”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“魅”字所在的面相对的面上标的字是( )| A. | 建 | B. | 力 | C. | 广 | D. | 安 |
 在平面直角坐标系中,顺次连接点A(-2,0)、B(0,3)、C(3,3)、D(4,0).
在平面直角坐标系中,顺次连接点A(-2,0)、B(0,3)、C(3,3)、D(4,0).
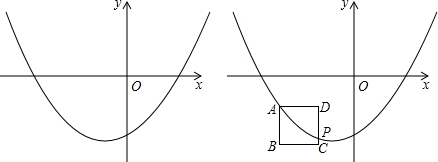
 如图,△ABC中,AB=AC,O是BC的中点,⊙O与AB相切于点D,求证:AC是⊙O的切线.
如图,△ABC中,AB=AC,O是BC的中点,⊙O与AB相切于点D,求证:AC是⊙O的切线.