题目内容
16. 没有量角器,利用刻度尺或三角板也能画出一个角的平分线吗?下面是小彬的做法,他的画法正确吗?请说明理由.
没有量角器,利用刻度尺或三角板也能画出一个角的平分线吗?下面是小彬的做法,他的画法正确吗?请说明理由.如图,①利用三角板在∠AOB的边上,分别取OM=ON.
②分别过M、N画OM、ON的垂线,交点为P.
③画射线OP.所以射线OP为∠AOB的角平分线.
分析 根据题意得出Rt△MOP≌Rt△NOP(HL),进而得出射线OP为∠AOB的角平分线.
解答 解:正确,
理由:在Rt△MOP和Rt△NOP中
∵$\left\{\begin{array}{l}{OP=OP}\\{MO=NO}\end{array}\right.$,
∴Rt△MOP≌Rt△NOP(HL),
∴∠MOP=∠NOP,
即射线OP为∠AOB的角平分线.
点评 此题主要考查了复杂作图以及全等三角形的判定与性质,得出Rt△MOP≌Rt△NOP是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.$\sqrt{6}$+2和$\sqrt{6}$-2的关系是( )
| A. | 互为相反数 | B. | 互为倒数 | C. | 相等 | D. | 以上都不对 |
7.点A(-3,-2)向上平移2个单位,再向左平移2个单位到点B,则点B的坐标为( )
| A. | (1,0) | B. | (-1,-4) | C. | (-1,0) | D. | (-5,0) |
4.下列说法中:①三角形中至少有2个角是锐角;②各边都相等的多边形是正多边形;③钝角三角形的三条高交于一点;④两个等边三角形全等;⑤三角形两个内角的平分线的交点到三角形三边的距离相等,正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.在平面中,下列说法正确的是( )
| A. | 四边相等的四边形是正方形 | |
| B. | 四个角相等的四边形是矩形 | |
| C. | 对角线相等的四边形是菱形 | |
| D. | 对角线互相垂直的四边形是平行四边形 |
6.一个直角三角形两直角边的比为3:2,斜边上的高分得的两个直角三角形的面积分别为S1和S2(S1<S2),则S1:S2=( )
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{2}$ |
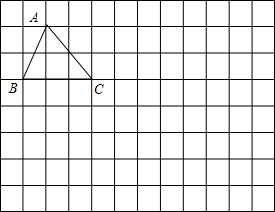 将如图所示的三角形ABC,先水平向右平移5格得三角形DEF,再竖直向下平移4格得到三角形GHQ,作出这两个三角形,并标上字母.
将如图所示的三角形ABC,先水平向右平移5格得三角形DEF,再竖直向下平移4格得到三角形GHQ,作出这两个三角形,并标上字母. 已知等腰Rt△ABC与等腰Rt△DBE,F为AE中点,G为CD中点,连结GF.判断FG与DC的位置关系和数量关系.
已知等腰Rt△ABC与等腰Rt△DBE,F为AE中点,G为CD中点,连结GF.判断FG与DC的位置关系和数量关系.