题目内容
8.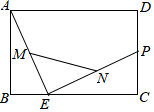 如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,点M、N分别是AE、PE的中点,则线段MN长为( )
如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,点M、N分别是AE、PE的中点,则线段MN长为( )| A. | 2$\sqrt{10}$ | B. | 3 | C. | $\sqrt{13}$ | D. | $\sqrt{10}$ |
分析 连接AP,根据矩形的性质求出AP的长度,再根据三角形的中位线平行于第三边并且等于第三边的一半可得MN=$\frac{1}{2}$AP,问题得解.
解答 解:连接AP,
∵矩形ABCD中,AB=DC=4,P是CD边上的中点,
∴DP=2,
∴AP=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
连接AP,
∵M,N分别是AE、PE的中点,
∴MN是△AEP的中位线,
∴MN=$\frac{1}{2}$AP=$\sqrt{10}$.
故选D.
点评 本题考查了矩形的性质,三角形的中位线平行于第三边并且等于第三边的一半,熟记性质以及定理并求出AP的值是解题的关键.

练习册系列答案
相关题目
19.某袋子装有一枚$10硬币、两枚$5硬币及一枚$2硬币,从该袋子中同时随机抽出两枚硬币.
(a)完成表,以展示抽出的两枚硬币的总金额的所有可能结果.
(b)求抽出的两枚硬币的总金额多于$7的概率.
(a)完成表,以展示抽出的两枚硬币的总金额的所有可能结果.
(b)求抽出的两枚硬币的总金额多于$7的概率.
| 总金额($) | $10 | $5 | $5 | $2 |
| $10 | 20 | 15 | 15 | 12 |
| $5 | 15 | 10 | 10 | 7 |
| $5 | 15 | 10 | 10 | 7 |
| $2 | 12 | 7 | 7 | 4 |
3.若将点A(2,3)向左平移3个单位,再向下平移4个单位,得到点B,则点B的坐标为( )
| A. | (5,-1) | B. | (-1,-1) | C. | (5,7) | D. | (-1,7) |
17.甲、乙两名同学进行射击练习,在相同条件下各射靶10次,将射击结果作统计如下:
(1)请你填上表中乙同学的有关数据;
(2)根据你所学的统计知识,利用上述某些数据评价甲、乙两人的射击水平.
| 命中环数 | 5 | 6 | 7 | 8 | 9 | 10 | 平均数 | 众数 | 方差 |
| 甲命中环数的次数 | 1 | 4 | 2 | 1 | 1 | 1 | 7 | 6 | 2.2 |
| 乙命中环数的次数 | 1 | 2 | 4 | 2 | 1 | 0 |
(2)根据你所学的统计知识,利用上述某些数据评价甲、乙两人的射击水平.
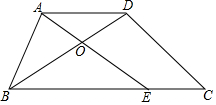 如图,在梯形ABCD中,AB=AD=5cm,CD=6cm,BC=10cm,E是BC上的一个动点,当四边形AECD为平行四边形时,OA的长为3cm.
如图,在梯形ABCD中,AB=AD=5cm,CD=6cm,BC=10cm,E是BC上的一个动点,当四边形AECD为平行四边形时,OA的长为3cm.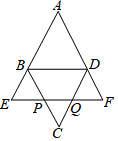 如图,平行四边形ABCD中,EF∥BD,分别交BC,CD于P,Q,交AB,AD的延长线于点E、F.
如图,平行四边形ABCD中,EF∥BD,分别交BC,CD于P,Q,交AB,AD的延长线于点E、F.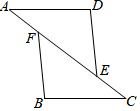 如图,点E、F在AC上,AD∥CB,且AD=CB,AF=CE.求证:△ADE≌△CBF.
如图,点E、F在AC上,AD∥CB,且AD=CB,AF=CE.求证:△ADE≌△CBF.