题目内容
19.某袋子装有一枚$10硬币、两枚$5硬币及一枚$2硬币,从该袋子中同时随机抽出两枚硬币.(a)完成表,以展示抽出的两枚硬币的总金额的所有可能结果.
(b)求抽出的两枚硬币的总金额多于$7的概率.
| 总金额($) | $10 | $5 | $5 | $2 |
| $10 | 20 | 15 | 15 | 12 |
| $5 | 15 | 10 | 10 | 7 |
| $5 | 15 | 10 | 10 | 7 |
| $2 | 12 | 7 | 7 | 4 |
分析 (1)列表法完成表格即可;
(2)根据概率公式求解可得.
解答 解:(1)两枚硬币的总金额的所有可能结果如下表:
| 总金额($) | $10 | $5 | $5 | $2 |
| $10 | 20 | 15 | 15 | 12 |
| $5 | 15 | 10 | 10 | 7 |
| $5 | 15 | 10 | 10 | 7 |
| $2 | 12 | 7 | 7 | 4 |
∴抽出的两枚硬币的总金额多于$7的概率为$\frac{11}{16}$.
点评 本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
9.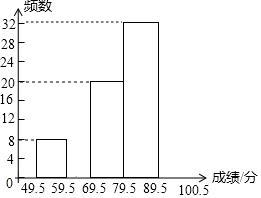 6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频数分布表和不完整的频数分布直方图如下:
6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频数分布表和不完整的频数分布直方图如下:
(1)直接写出a的值,并补全频数分布表和频数分布直方图.
(2)若成绩在80分以上为优秀,求这次参赛的学生中成绩为优秀的约有多少人?
 6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频数分布表和不完整的频数分布直方图如下:
6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频数分布表和不完整的频数分布直方图如下:| 分组 | 频数 | 所占百分比 |
| 49.5~59.5 | 8 | 8% |
| 59.5~69.5 | 12 | 12% |
| 69.5~79.5 | 20 | 20% |
| 79.5~89.5 | 32 | 32% |
| 89.5~100.5 | 28 | a |
(2)若成绩在80分以上为优秀,求这次参赛的学生中成绩为优秀的约有多少人?
14.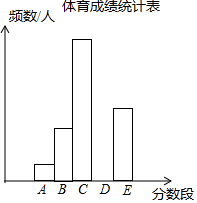 为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.
为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.
根据上面的信息,回答下列问题:
(1)统计表中,a=0.15,b=60,c=240;将频数分布直方图补充完整.
(2)小明说:“这组数据的众数一定在C中.”你认为小明的说法正确吗?错误(选填“正确”或“错误”).
(3)若成绩在27分及以上定为优秀,则该市30000名九年级学生中体育成绩为优秀的学生人数约有多少?
 为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.
为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.| 分数段 | A | B | C | D | E | 合计 |
| 频数/人 | 12 | 36 | 84 | b | 48 | c |
| 频率 | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
(1)统计表中,a=0.15,b=60,c=240;将频数分布直方图补充完整.
(2)小明说:“这组数据的众数一定在C中.”你认为小明的说法正确吗?错误(选填“正确”或“错误”).
(3)若成绩在27分及以上定为优秀,则该市30000名九年级学生中体育成绩为优秀的学生人数约有多少?
8.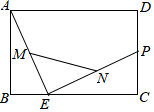 如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,点M、N分别是AE、PE的中点,则线段MN长为( )
如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,点M、N分别是AE、PE的中点,则线段MN长为( )
 如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,点M、N分别是AE、PE的中点,则线段MN长为( )
如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,点M、N分别是AE、PE的中点,则线段MN长为( )| A. | 2$\sqrt{10}$ | B. | 3 | C. | $\sqrt{13}$ | D. | $\sqrt{10}$ |
 在平面直角坐标系xOy中,已知一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B.
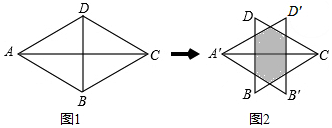
在平面直角坐标系xOy中,已知一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B. 如图,若$\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}=\frac{3}{2}$,且△ABC的周长为36cm,则△ADE的周长为24cm.
如图,若$\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}=\frac{3}{2}$,且△ABC的周长为36cm,则△ADE的周长为24cm.