题目内容
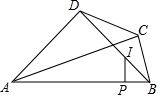
15. 如图,在四边形ABCD中,AB=DC,延长线段CB到E,使BE=AD,连接AE,AC,∠ADC+∠ABC=180°.
如图,在四边形ABCD中,AB=DC,延长线段CB到E,使BE=AD,连接AE,AC,∠ADC+∠ABC=180°.求证:(1)△ABE≌△CDA
(2)AD∥EC.
分析 (1)先依据同角的补角相等可证明∠ADC=∠ABE,然后依据SAS可证明△ABE≌△CDA;
(2)由全等三角形的性质可得到∠E=∠CAD,AE=AC,然后依据等腰三角形的性质可得到∠E=∠ACE,通过等量代换可得到∠CAD=∠ACE,最后依据平行线判定定理进行证明即可.
解答 解:(1)∵∠ADC+∠ABC=180°,∠ABE+∠ABC=180°,
∴∠ADC=∠ABE.
在△ABE和△CDA中$\left\{\begin{array}{l}{AB=DC}\\{∠ADC=∠ABE}\\{BE=AD}\end{array}\right.$,
∴△ABE≌△CDA.
(2)∵△ABE≌△CDA,
∴∠E=∠CAD,AE=AC.
∴∠E=∠ACE.
∴∠CAD=∠ACE.
∴AD∥EC.
点评 本题主要考查的是全等三角形的性质与判定、等腰三角形的性质,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
20. 如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,6),⊙C的半径长为5,则C点坐标为( )
如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,6),⊙C的半径长为5,则C点坐标为( )
 如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,6),⊙C的半径长为5,则C点坐标为( )
如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,6),⊙C的半径长为5,则C点坐标为( )| A. | (3,4) | B. | (4,3) | C. | (-4,3) | D. | (-3,4) |
 如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,…将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,…则顶点M2017的坐标为(4033,4033).
如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,…将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,…则顶点M2017的坐标为(4033,4033).
 如图,Rt△ABC中,∠ACB=90°,CD为△ABC的外角平分线且∠ADB=90°.
如图,Rt△ABC中,∠ACB=90°,CD为△ABC的外角平分线且∠ADB=90°. 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题: 如图,PA、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.
如图,PA、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.